Ответы
Ответ дал:
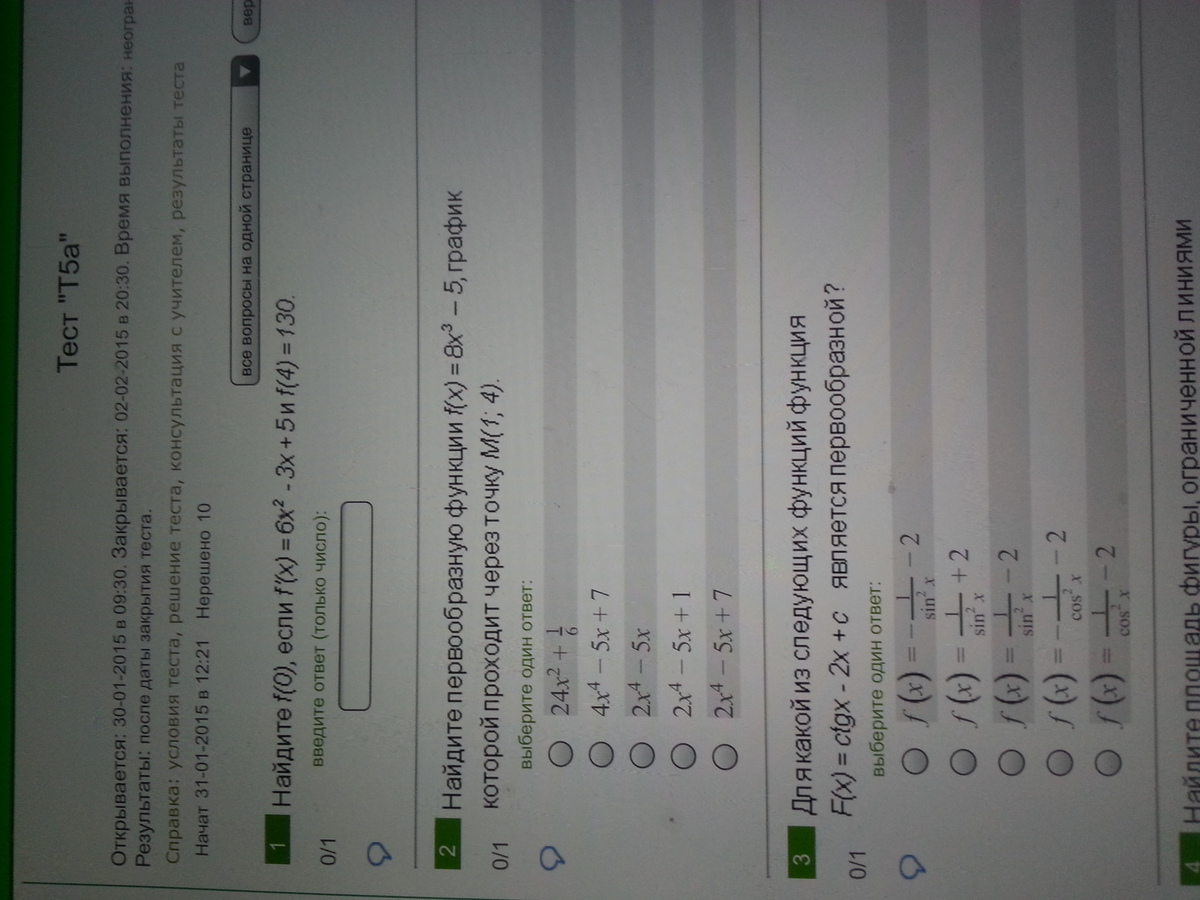
1
f(4)=130 ⇒ 2*4³-3/2*4²+5*4+C=130
128-24+20+C=130 ⇒ C=6 ⇒
f(x)=2x³-3/2x²+5x+6 ⇒ f(0)=2*0³-3/2*0²+5*0+6 ⇒
f(0)=6
мэрикэй2000:
Спасибо, скажи, а где ты это решаешь? это приложение или ты сам?
я сам решаю
не мог бы ты решить еще те ,что на фото
Похожие вопросы
1 год назад
1 год назад
2 года назад
7 лет назад
8 лет назад