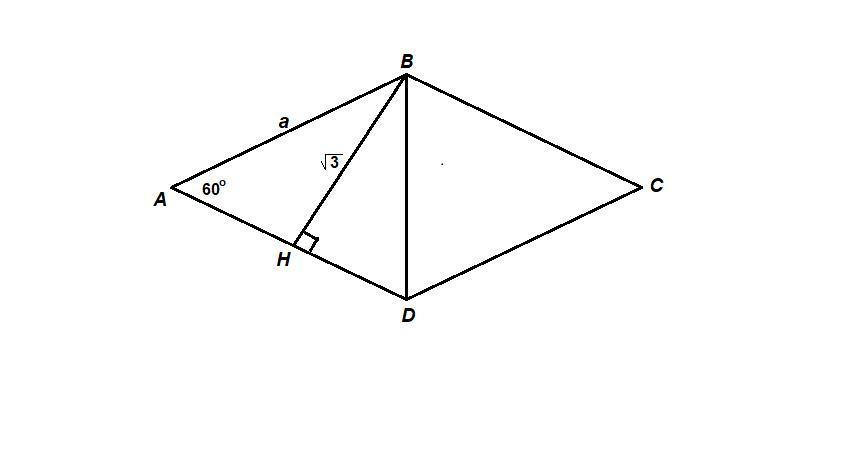
В ромбе один из углов равен 60 градусов . Высота ромба равна √3 . Найдите длину меньшей диагонали .

Дано:

АВСД-ромб

угол B=60 град

высота СН=sqrt{3}

Найти: АС

Решение:

1. Расмотрим треугольник СНВ. В нём ВС=СН/sin B=sqrt{3}/(sqrt{3}/2))=2

2.Рассмотрим треугольник АВС. Он равнобедренный, АВ=ВС как стороны ромба,

   угол В=60 град, следовательно угол А=углу С=60 град. Это означает, что АВС-равносторонний треугольник и АС=АВ=ВС=2

Ответ:2

Ответ:   2

Объяснение:

В ΔABD АВ = AD как стороны ромба, значит треугольник равнобедренный, тогда ∠В = ∠D = (180° - 60°)/2 = 60°, т.е. треугольник равносторонний.

Высота равностороннего треугольника:

ВН = BD√3/2

BD = 2BH / √3 =  2