Через точку D , лежащую между
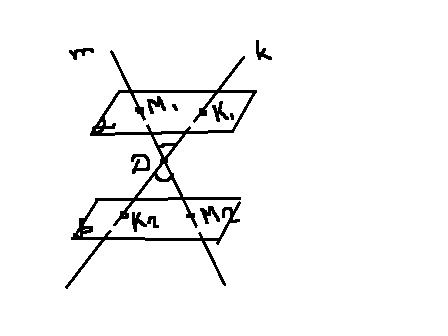
параллельными плоскостями альфа и бета , проведены прямые m и k . Прямая m пересекает плоскости альфа и бета в точках М1 и М2 соответственно, а прямая k - в точках К1 и К2 соответственно. Вычислите длину отрезка DM2 , если М1М2=20 дм , М1К1:М2К2 = 3:7
СРОООЧНООО ПЖС )))((((