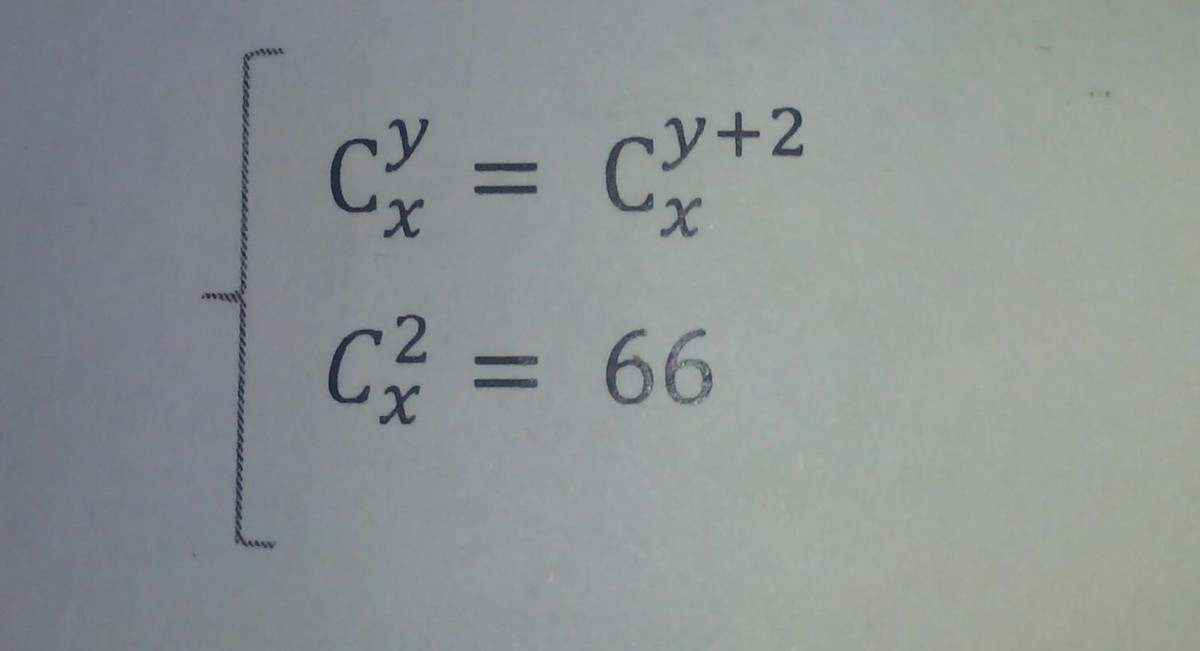Ответы
Ответ дал:
0
Сначала решаем второе уравнение, расписывая число сочетаний по формуле:
![C_x^2=66;\
frac{x!}{2!*(x-2)!}=66;\
frac{x*(x-1)*(x-2)!}{2*(x-2)!}=66;\
x(x-1)=66*2.](https://tex.z-dn.net/?f=C_x%5E2%3D66%3B%5C%0Afrac%7Bx%21%7D%7B2%21%2A%28x-2%29%21%7D%3D66%3B%5C%0Afrac%7Bx%2A%28x-1%29%2A%28x-2%29%21%7D%7B2%2A%28x-2%29%21%7D%3D66%3B%5C%0Ax%28x-1%29%3D66%2A2. "C_x^2=66;\
frac{x!}{2!*(x-2)!}=66;\
frac{x*(x-1)*(x-2)!}{2*(x-2)!}=66;\
x(x-1)=66*2.")
Последнее уравнение - квадратное, его корни 12 и (-11), но поскольку отрицательные числа в комбинаторике не рассматриваются, то x=12.
Теперь находим y из первого уравнения:
![C_{12}^y=C_{12}^{y+2};\
frac{12!}{y!*(12-y)!}=frac{12!}{(y+2)!*(10-y)!};\](https://tex.z-dn.net/?f=C_%7B12%7D%5Ey%3DC_%7B12%7D%5E%7By%2B2%7D%3B%5C%0Afrac%7B12%21%7D%7By%21%2A%2812-y%29%21%7D%3Dfrac%7B12%21%7D%7B%28y%2B2%29%21%2A%2810-y%29%21%7D%3B%5C "C_{12}^y=C_{12}^{y+2};\
frac{12!}{y!*(12-y)!}=frac{12!}{(y+2)!*(10-y)!};\")
Числители одинаковы, знаменатели всегда положительны, значит, знаменатели равны:
![y!*(12-y)!=(y+2)!*(10-y)!;\
y!*((12-y)*(11-y)*(10-y)!)=((y+2)*(y+1)*y!)*(10-y)!;\
(12-y)(11-y)=(y+1)(y+2);\
y^2-23y+132=y^2+3y+2;\
130=26y;\
y=5.](https://tex.z-dn.net/?f=y%21%2A%2812-y%29%21%3D%28y%2B2%29%21%2A%2810-y%29%21%3B%5C%0Ay%21%2A%28%2812-y%29%2A%2811-y%29%2A%2810-y%29%21%29%3D%28%28y%2B2%29%2A%28y%2B1%29%2Ay%21%29%2A%2810-y%29%21%3B%5C%0A%2812-y%29%2811-y%29%3D%28y%2B1%29%28y%2B2%29%3B%5C%0Ay%5E2-23y%2B132%3Dy%5E2%2B3y%2B2%3B%5C%0A130%3D26y%3B%5C%0Ay%3D5. "y!*(12-y)!=(y+2)!*(10-y)!;\
y!*((12-y)*(11-y)*(10-y)!)=((y+2)*(y+1)*y!)*(10-y)!;\
(12-y)(11-y)=(y+1)(y+2);\
y^2-23y+132=y^2+3y+2;\
130=26y;\
y=5.")
Так как полученное y - целое неотрицательное, то оно действительно является решением.
Ответ: (12, 5)
Последнее уравнение - квадратное, его корни 12 и (-11), но поскольку отрицательные числа в комбинаторике не рассматриваются, то x=12.
Теперь находим y из первого уравнения:
Числители одинаковы, знаменатели всегда положительны, значит, знаменатели равны:
Так как полученное y - целое неотрицательное, то оно действительно является решением.
Ответ: (12, 5)
Ответ дал:
0
Спасибо большое!
Похожие вопросы
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад