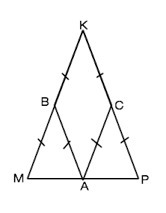
В равнобедренном треугольнике MPK с основанием MP проведены средние линии AB и AC (А принадлежит MP, B принадлежит MK, C принадлежит PK). Определите вид
четырехугольника BKCA, если KP=12 см

Можете с решением?

Теорема: Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей и равна её половине.

∆ МКР равнобедренный. МК=КР=12 см ⇒

АВ||КР; АВ=0,5•КР=12:2=6 см

АС||КМ; АС=0,5•КМ=6 см

Противоположные стороны АВКС параллельны, ⇒АВКС - параллелограмм.

ВК=КВ=СА=АВ

Четырехугольник ВКСА – ромб.