Ответы
Ответ дал:
0
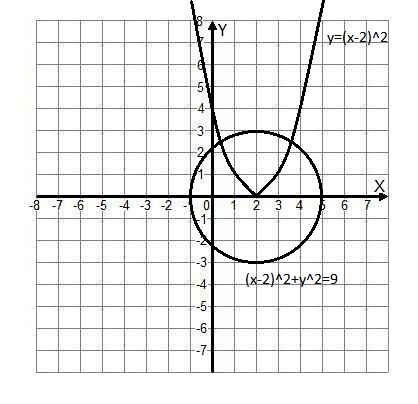
Дальше получается что координаты точек пересечения этих графиков будут нецелыми числами (это видно и по графику):
Приложения:
Ответ дал:
0
{ (x-2)^2+y^2=9,
y=x^2-4x+4,
{y=(x-2)^2,
(x-2)^2+(x-2)^4=9,
(x-2)^4+(x-2)^2-9=0,
(x-2)^2=t,
t^2+t-9=0,
D=37,
t1=(-1-√37)/2<0,
t2=(-1+√37)/2,
(x-2)^2=(-1+√37)/2,
Уверена что в условии нет ошибки?
Приложения:

Похожие вопросы
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад