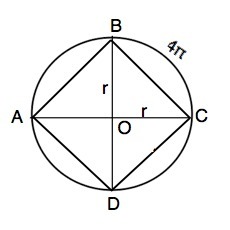
Диаметр окружности AC и BD пересекаются под углом 90 .Длина дуги Bc равна 4π см. Найдите: радиус окружности; длины хорд с концами в точках A, B, C, D.
Ответы
Ответ дал:
0
Так как диаметры пересекаются под прямым углом, они при пересечении делят окружность на 4 равных сектора. Тогда длина окружности – четыре дуги ВС и равна 16π
Из формулы длины окружности С=2πr
r=16π:2π=8 см
Длина каждой из указанных хорд равна гипотенузе равнобедренного треугольника с катетами, равным r=8
AB=BC=CD=DA=√(AO²+BO²)=√(2•8²)=8√2
Приложения:
Похожие вопросы
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад