2. Какой четверти числовой окружности принадлежит точка, соответствующая числу: а) 4; б) 8 в) – 9; г) 31?

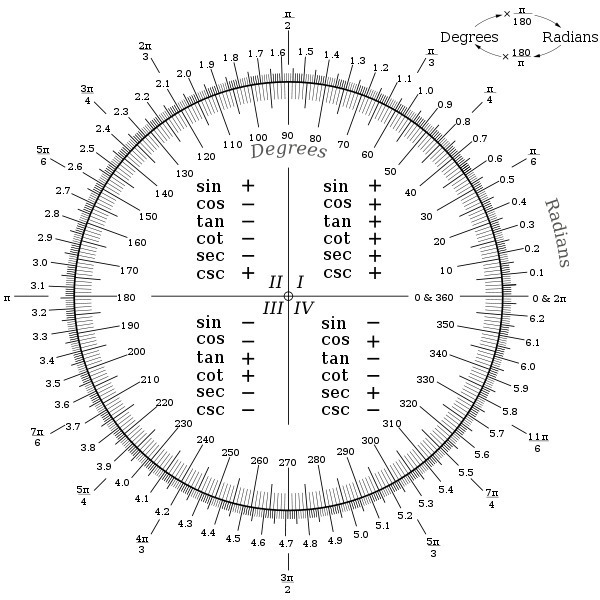
В приложении, картинка для быстрого понимания.

Во первых число, которое дано в задании является радианной мерой угла.

Если начинать отсчет против часовой стрелки (угол положителен), и повернуть на 180 градусов (полуокружность), то в радианах это будет . Т.е. в 180 градусах вмещается приблизительно 3 радиана.
Найдем приблизительно, сколько радиан в 90 градусах:


- радиан.

Следовательно при повороте на 
имеем 4,5 радиан.
Значит, 4 радиана находиться где то между  . Т.е. в 3 четверти.

2)
Найдем количество оборотов на 90 градусов для числа 8:
 
Т.е. мы делаем полный оборот (он равен приблизительно 4 оборотам на 90 градусов) + один оборот на 90 градусов  + оборот на 0.3 радиана. 
Следовательно 8 находиться в 2 четверти.

3)
Здесь мы делаем обороты по часовой стрелке (угол отрицателен).
Снова находим количество оборотов :


т.е. приблизительно шесть оборотов по часовой стрелке.
Это 1 полный оборот, + оборот на 180 градусов. 
То есть, -9 радиан находится где то на 3 четверти.

 4)



Приблизительно 5,15 полных оборотов. Т.е. 5 полных оборотов + оборот на 0.15 радиан.
Т.е. 31 находится где то на 1 четверти.