Ответы
Ответ дал:
0
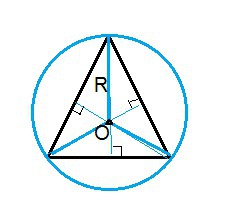
Центр описанной вокруг треугольника окружности находится на пересечении срединных перпендикуляров. Вокруг правильного треугольника - на пересечении его высот ( они его срединные перпендикуляры).
Радиус описанной вокруг правильного (равностороннего) треугольника окружности равен 2/3 его высоты, и равен а/√3.
a=√3
R=√3/√3=1см
Радиус описанной вокруг правильного (равностороннего) треугольника окружности равен 2/3 его высоты, и равен а/√3.
a=√3
R=√3/√3=1см
Приложения:
Ответ дал:
0
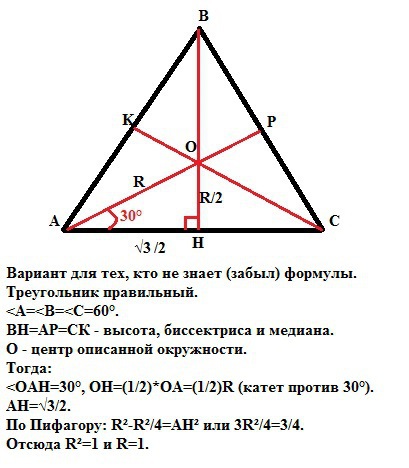
Вариант для тех, кто не знает (забыл) формулы .
Треугольник правильный.
<A=<B=<C=60°.
ВН=АР=СК - высота, биссектриса и медиана.
О - центр описанной окружности.
Тогда:
<OAH=30°, ОН=(1/2)*ОА=(1/2)R (катет против 30°).
АН=√3/2.
По Пифагору: R²-R²/4=AH² или 3R²/4=3/4.
Отсюда R²=1 и R=1.
Треугольник правильный.
<A=<B=<C=60°.
ВН=АР=СК - высота, биссектриса и медиана.
О - центр описанной окружности.
Тогда:
<OAH=30°, ОН=(1/2)*ОА=(1/2)R (катет против 30°).
АН=√3/2.
По Пифагору: R²-R²/4=AH² или 3R²/4=3/4.
Отсюда R²=1 и R=1.
Приложения:
Похожие вопросы
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад