Студент и студентка условились встретиться в определенном месте между 12 и 13 часами дня. Девушка, пришедшая первой, ждет юношу не более 5 минут, после уходит. Юноша, пришедший первым, ждет девушку не более 30 минут, после чего уходит. Найти вероятность того, что встреча состоится, если каждый из них наудачу выбирает момент своего прихода. Плииииз)*

Пусть момент прихода юноши - это x, момент прихода девушки - y. При этом 0 соответствует 12 часам дня, а 1 - 12:05 и так далее до 12, соответствуещего 13:00. На координатной плоскости множество всех возможных событий - это квадрат, заданный условиями . Теперь найдем, каким точкам соответствует событие "встреча состоялась". Дополнительно ко всему нижеследующему налагается условие, что точки вне квадрата не рассматриваются.
1) Условие того, что девушка не уйдет раньше прихода юноши: . Заметим, что условие также выполняется, если юноша приходит первым, т.к. тогда правая часть отрицательна.
2) Аналогично рассматриваем условие, что юноша не уйдет раньше: .

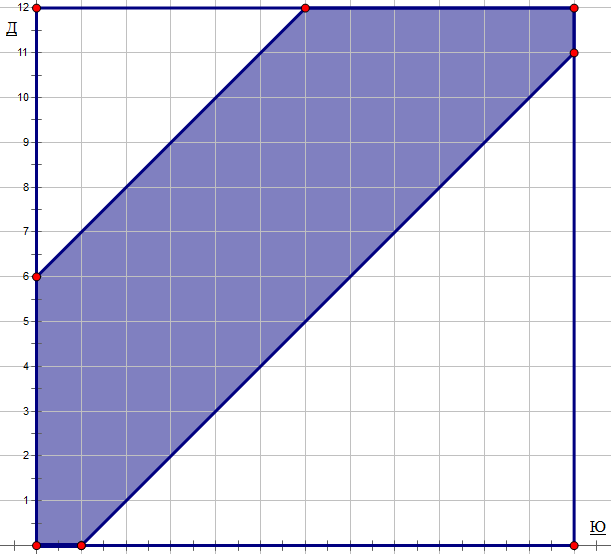
Оба условия должны выполняться одновременно, поэтому фигура, составленная из точек, для которых встреча происходит - это промежуток между прямыми y=x-1; y=x+6, на рисунке отмечена синим. Искомая вероятность равна отношению площади этой фигуры к площади квадрата. Это отношение можно искать по-разному, ответ получается .