На стороне АС как на основании по одну сторону от нее построены два равнобедренных треугольника АВС и АМС. Прямая ВМ пересекает сторону АС в точке Е.Найдите длину отрезка СЕ, если периметр треугольника АМС равен 30 см, а его основание на 3 см больше боковой стороны. Прошу, помогите!! Очень срочно!!!
Ответы
Ответ дал:
0
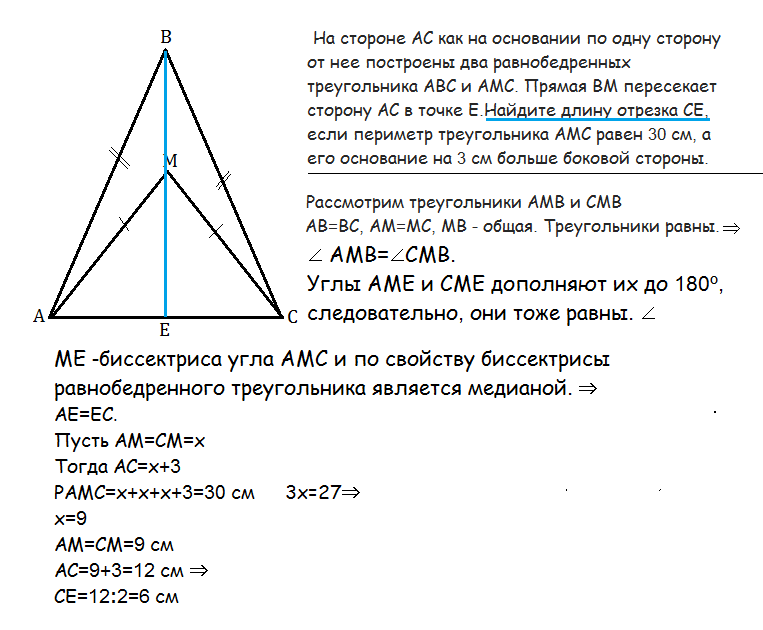
На стороне АС как на основании по одну сторону от нее построены два равнобедренных треугольника АВС и АМС. Прямая ВМ пересекает сторону АС в точке Е. Найдите длину отрезка СЕ, если периметр треугольника АМС равен 30 см, а его основание на 3 см больше боковой стороны.
---------
Рассмотрим треугольники АМВ и СМВ
АВ=ВС, АМ=МС, МВ - общая. Эти треугольники равны. ⇒
∠ АМВ=∠СМВ.
Углы АМЕ и СМЕ дополняют их до 180º, следовательно, они тоже равны.⇒
МЕ -биссектриса угла АМС и по свойству биссектрисы равнобедренного треугольника является медианой. ⇒
АЕ=ЕС.
Пусть АМ=СМ=х
Тогда АС=х+3
Р Δ АМС=х+х+х+3=30 см
х=9
АМ=СМ=9 см
АС=9+3=12 см
СЕ=12:2=6 см
---------
Рассмотрим треугольники АМВ и СМВ
АВ=ВС, АМ=МС, МВ - общая. Эти треугольники равны. ⇒
∠ АМВ=∠СМВ.
Углы АМЕ и СМЕ дополняют их до 180º, следовательно, они тоже равны.⇒
МЕ -биссектриса угла АМС и по свойству биссектрисы равнобедренного треугольника является медианой. ⇒
АЕ=ЕС.
Пусть АМ=СМ=х
Тогда АС=х+3
Р Δ АМС=х+х+х+3=30 см
х=9
АМ=СМ=9 см
АС=9+3=12 см
СЕ=12:2=6 см
Приложения:
Похожие вопросы
2 года назад
2 года назад
7 лет назад
10 лет назад
10 лет назад