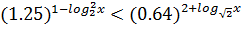Ответы
Ответ дал:
0
Ответ дал:
0
поставим t = loq_2 X
1,25 =5/4=(4/5)^(-1) =0,8^(-1) ; 0,64 =64/100 = (8/10)^2 =0,8²
получаем
0,8^(t² - 1) < (0,8)^2(2 + 2t) [ loq_√2 X =loq_2 X /(1/2) =2loq_2 X =2t ]
т.к . 0< 0,8 <1 ==> t² - 1 > 4t+4 ==> t² - 4t - 5 !0 ==> t∈(-∞ ;-1) U (5;∞)
loq_2 X < -1 ==> 0< x <1/2 , т.е. x∈ (0 ; 0,5)
[ т.к . основание логарифма 2 больше 1]
loq_2 X > 5 ==>x > 2^5 =32 , т.е x∈ (32 ; ∞)
ответ: x∈ (0 ; 0,5) U (32 ; ∞)
1,25 =5/4=(4/5)^(-1) =0,8^(-1) ; 0,64 =64/100 = (8/10)^2 =0,8²
получаем
0,8^(t² - 1) < (0,8)^2(2 + 2t) [ loq_√2 X =loq_2 X /(1/2) =2loq_2 X =2t ]
т.к . 0< 0,8 <1 ==> t² - 1 > 4t+4 ==> t² - 4t - 5 !0 ==> t∈(-∞ ;-1) U (5;∞)
loq_2 X < -1 ==> 0< x <1/2 , т.е. x∈ (0 ; 0,5)
[ т.к . основание логарифма 2 больше 1]
loq_2 X > 5 ==>x > 2^5 =32 , т.е x∈ (32 ; ∞)
ответ: x∈ (0 ; 0,5) U (32 ; ∞)
Приложения:
Похожие вопросы
2 года назад
2 года назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад