Предмет: Математика
Автор: sos905090
Вопрос задан 9 лет назад

помогите решить уравнения y=x2/2+5x+7/2

Ответы

Ответ дал: Trover

$y=frac{x^2}2+5x+frac72$
1. ООФ: $xinmathbb{R}$
2. Чётность/нечётность:
$y(-x)=frac{(-x)^2}2+5cdot(-x)+frac72=frac{x^2}2-5x+frac72Rightarrowbegin{cases}neq y(x)\neq-y(x)end{cases}$
Функция общего вида - ни чётная, ни нечётная.
3. Пересечение с осями:
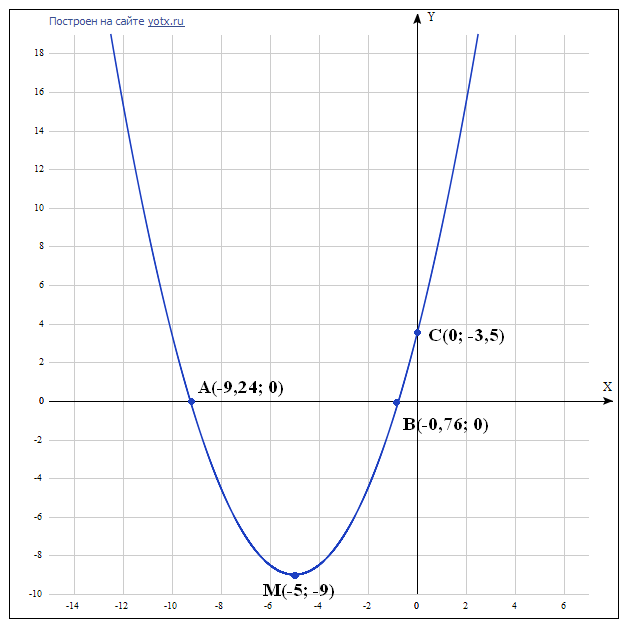
$c;OX,;y=0:\frac{x^2}2+5x+frac72=0;;times2\x^2+10x+7=0\D=100-4cdot7=72\x_{1,2}=frac{-10pmsqrt{72}}2=-5pm2sqrt18\x_1=-5-sqrt{18}approx-9,24\x_2=-5+sqrt{18}approx-0,76\\c;OY,;x=0\y=frac72=3,5$
Пересечение с осью OX в точках A(-9,24; 0) и B(-0,76; 0). Пересечение с осью OY в точке C(0; 3,5).
4. Асимптот нет.
5. Экстремумы и монотонность:
$y'=left(frac{x^2}2+5x+frac72right)'=frac{2x}2+5=x+5\x+5=0\x=-5$
Получаем 2 интервала: $(-infty;;-5);;u;;(-5;;+infty)$ . На первом интервале производная отрицательна, значит функция на нём убывает. На втором производная положительна, значит функция на нём возрастает.
Точка M (-5; -9) - точка минимума.
6. Точки перегиба, выпуклость и вогнутость:
$y''=(x-5)'=1$
Точек перегиба нет, функция вогнута на всей области существования.
7. График - см. вложение.

Приложения: