Ответы
Ответ дал:
1
Читай сначала 1 пункт, затем 2, 3, 4.У меня не вставляется в начало концовка решения.
![3)\; \; \left \{ {{5^{x}\geq 4} \atop {5^{x}\leq 125}} \right. \; \left \{ {{5^{x}\geq 5^{log_54}} \atop {5^{x}\leq 5^3}} \right. \; \left \{ {{x\geq log_54} \atop {x\leq 3}} \right. \\\\4)x\in [log_54;1)U[2;3)<br /><br />[tex]1)log_{x}(x^2-6x+9) \leq 0,\; ODZ:\; \left \{ {{x>0,x\ne 1} \atop {x^2-6x+9=(x-3)^2>0}} \right.\; \left \{ {{x>0,x\ne 1} \atop {x\ne 3}} \right. \\\\Metod\; racionalizacii:\; (x^2-6x+9-1)(x-1) \leq 0,\\\\(x-2)(x-4)(x-1) \leq 0,\\\\(0)---(1)+++[2]---(3)---[4]+++\\\\x\in (0,1)U[\, 2,3)U(3,4\, ]\\\\2)\; \; 25^{x-1}-129\cdot 5^{x-2}+20 \leq 0,\; \to \; 5^{2x-2}-129\cdot 5^{x}\cdot 5^{-2}+20 \leq 0\; |\cdot 25\\\\(5^{x})^2-129\cdot 5^{x}+20\cdot 25 \leq 0\; \to \; 5^{x}=t,\; t^2-129t+500 \leq 0 3)\; \; \left \{ {{5^{x}\geq 4} \atop {5^{x}\leq 125}} \right. \; \left \{ {{5^{x}\geq 5^{log_54}} \atop {5^{x}\leq 5^3}} \right. \; \left \{ {{x\geq log_54} \atop {x\leq 3}} \right. \\\\4)x\in [log_54;1)U[2;3)<br /><br />[tex]1)log_{x}(x^2-6x+9) \leq 0,\; ODZ:\; \left \{ {{x>0,x\ne 1} \atop {x^2-6x+9=(x-3)^2>0}} \right.\; \left \{ {{x>0,x\ne 1} \atop {x\ne 3}} \right. \\\\Metod\; racionalizacii:\; (x^2-6x+9-1)(x-1) \leq 0,\\\\(x-2)(x-4)(x-1) \leq 0,\\\\(0)---(1)+++[2]---(3)---[4]+++\\\\x\in (0,1)U[\, 2,3)U(3,4\, ]\\\\2)\; \; 25^{x-1}-129\cdot 5^{x-2}+20 \leq 0,\; \to \; 5^{2x-2}-129\cdot 5^{x}\cdot 5^{-2}+20 \leq 0\; |\cdot 25\\\\(5^{x})^2-129\cdot 5^{x}+20\cdot 25 \leq 0\; \to \; 5^{x}=t,\; t^2-129t+500 \leq 0](https://tex.z-dn.net/?f=3%29%5C%3B+%5C%3B++%5Cleft+%5C%7B+%7B%7B5%5E%7Bx%7D%5Cgeq+4%7D+%5Catop+%7B5%5E%7Bx%7D%5Cleq+125%7D%7D+%5Cright.++%5C%3B++%5Cleft+%5C%7B+%7B%7B5%5E%7Bx%7D%5Cgeq+5%5E%7Blog_54%7D%7D+%5Catop+%7B5%5E%7Bx%7D%5Cleq+5%5E3%7D%7D+%5Cright.+%5C%3B++%5Cleft+%5C%7B+%7B%7Bx%5Cgeq+log_54%7D+%5Catop+%7Bx%5Cleq+3%7D%7D+%5Cright.+%5C%5C%5C%5C4%29x%5Cin+%5Blog_54%3B1%29U%5B2%3B3%29%3Cbr+%2F%3E%3Cbr+%2F%3E%5Btex%5D1%29log_%7Bx%7D%28x%5E2-6x%2B9%29+%5Cleq+0%2C%5C%3B+ODZ%3A%5C%3B++%5Cleft+%5C%7B+%7B%7Bx%26gt%3B0%2Cx%5Cne+1%7D+%5Catop+%7Bx%5E2-6x%2B9%3D%28x-3%29%5E2%26gt%3B0%7D%7D+%5Cright.%5C%3B+++%5Cleft+%5C%7B+%7B%7Bx%26gt%3B0%2Cx%5Cne+1%7D+%5Catop+%7Bx%5Cne+3%7D%7D+%5Cright.+%5C%5C%5C%5CMetod%5C%3B+racionalizacii%3A%5C%3B+%28x%5E2-6x%2B9-1%29%28x-1%29+%5Cleq+0%2C%5C%5C%5C%5C%28x-2%29%28x-4%29%28x-1%29+%5Cleq+0%2C%5C%5C%5C%5C%280%29---%281%29%2B%2B%2B%5B2%5D---%283%29---%5B4%5D%2B%2B%2B%5C%5C%5C%5Cx%5Cin+%280%2C1%29U%5B%5C%2C+2%2C3%29U%283%2C4%5C%2C+%5D%5C%5C%5C%5C2%29%5C%3B+%5C%3B+25%5E%7Bx-1%7D-129%5Ccdot+5%5E%7Bx-2%7D%2B20+%5Cleq+0%2C%5C%3B+%5Cto+%5C%3B+5%5E%7B2x-2%7D-129%5Ccdot+5%5E%7Bx%7D%5Ccdot+5%5E%7B-2%7D%2B20+%5Cleq+0%5C%3B+%7C%5Ccdot+25%5C%5C%5C%5C%285%5E%7Bx%7D%29%5E2-129%5Ccdot+5%5E%7Bx%7D%2B20%5Ccdot+25+%5Cleq+0%5C%3B+%5Cto+%5C%3B+5%5E%7Bx%7D%3Dt%2C%5C%3B+t%5E2-129t%2B500+%5Cleq+0)

++++[4]----[125]+++ t Є [4,125]
++++[4]----[125]+++ t Є [4,125]
Ответ дал:
1
Решение в файлах. Будут вопросы - спрашивайте ))
 Пусть
Пусть  , t>=0.
, t>=0.
 .
D=16641-2000=14641=121^2.
t1=(129+121)/2=125. t2=(129-121)/2=4.
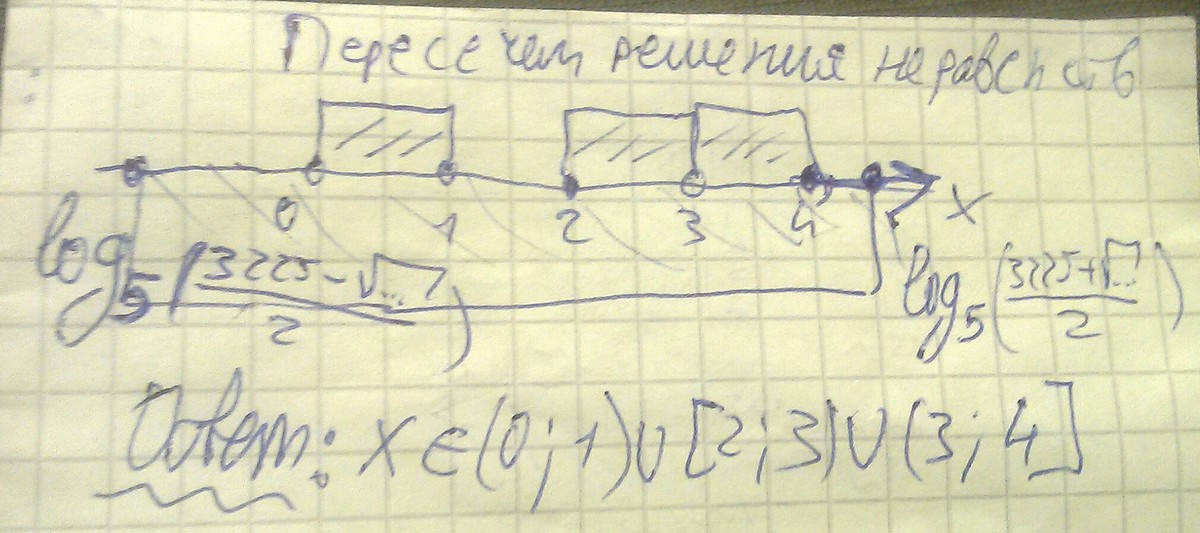
Значит, (t-125)(t-4)<=0. Получаем, что t принадлежит отрезку [4;125], тогда х принадлежит отрезку [log_5_4;3]. Пересекая это решение с решением первого неравенства получим как раз, что х принадлежит [log_5_4;1) и [2;3).
.
D=16641-2000=14641=121^2.
t1=(129+121)/2=125. t2=(129-121)/2=4.
Значит, (t-125)(t-4)<=0. Получаем, что t принадлежит отрезку [4;125], тогда х принадлежит отрезку [log_5_4;3]. Пересекая это решение с решением первого неравенства получим как раз, что х принадлежит [log_5_4;1) и [2;3).
Приложения:


Zhiraffe:
Тьфу, минус два не заметил у пятерки в степени
вообще в ответе должно получиться [log_5_4;1); [2;3), но идею с основанием я упустила... перерешаем. спасибо)))
Я с ноута позже зайду и удалю второй и третий файл, не имеющие отношения у задаче
Похожие вопросы
1 год назад
7 лет назад
7 лет назад
8 лет назад