ПОМОГИТЕ,ПОЖАЛУСТА!!!СРОЧНО!!!
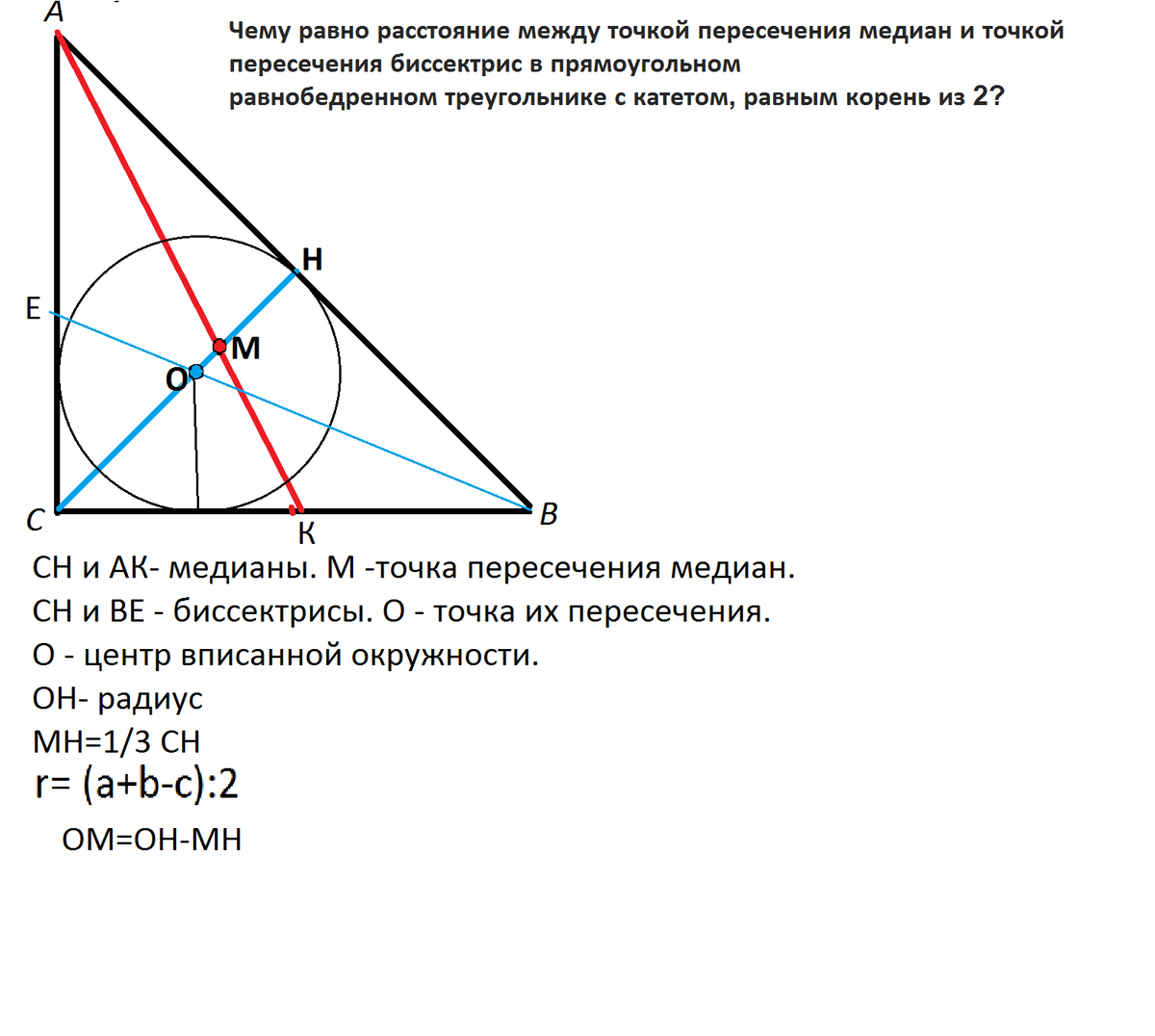
Чему равно расстояние между точкой пересечения медиан и точкой пересечения биссектрис в прямоугольном равнобедренном треугольнике с катетом, равным корень из 2?
Очень нужна помошь!!!!
Ответы
Можно обойтись и без рисунка, но для наглядности он дан.
Заметим, что в равнобедренном треугольнике биссектриса и медиана, проведенные к основанию, совпадают.
Поэтому СН и АК - медианы и пересекаются с точке М.
Биссектрисы пересекаются в точке О, и эта точка - центр вписанной окружности. Искомое расстояние - ОМ.
В треугольнике АВС гипотенуза
АВ = СВ:sin(45°)=2
CН -медиана и равна половине гипотенузы по свойству медианы прямоугольного треугольника.
СН=1
Медианы треугольника точкой пересечения делятся в отношении 2:1 считая от вершины.
⇒МН- одна треть медианы СН =1/3
ОМ=ОН-МН.
ОН=r= радиус вписанной в АВС окружности.
r=(a+b-c):2= (2√2-2):2=√2-1
ОМ=√2-1-1/3= √2-1¹/₃ = приближенно 0,08088