Помогите решить, пожалуйста (вложения)

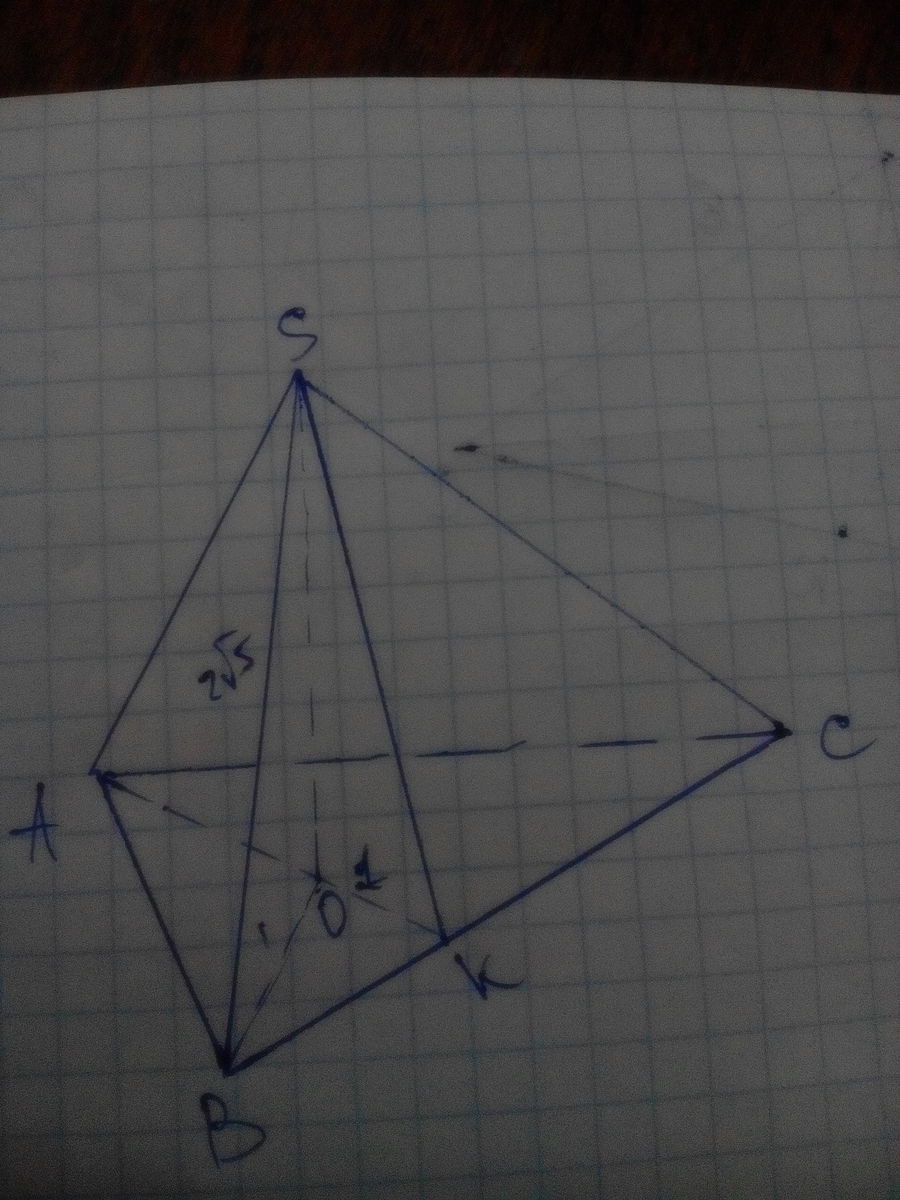
r=OH=1см
OH=1/3CH⇒CH=3
AC=CH/sin60=3:√3/2=3*2√3=2√3
AH=BH=√3
l=SA=2√5
SH=√(SA²-AH²)=√(20-3)=√17
Sбок=1/2P*SH=1/2*3*AA*SH=1/2*3*2√3*√17=3√51

по определению радиусу вписанной окружности в правильный треугольник, сторона треугольника

r=a/(2√3)
AB=2√3•r=2√3 см

Радиус вписанной окружности OB
R=a/√3
OB=2√3/√3=2 см

С прямоугольного треугольника SBO(угол SOB=90°)
по т. Пифагора
SO=√(SB²-OB²)=√(20-4)=4 см

С прямоугольного треугольника SKO(угол SOK=90°)
SK=√(1²+4²)=√17 см


Площадь боковой поверхности:

Sб=1/2*Pосн *SK=1/2*3*2√3*√17=3√51 см²

Ответ: 3√51 см².