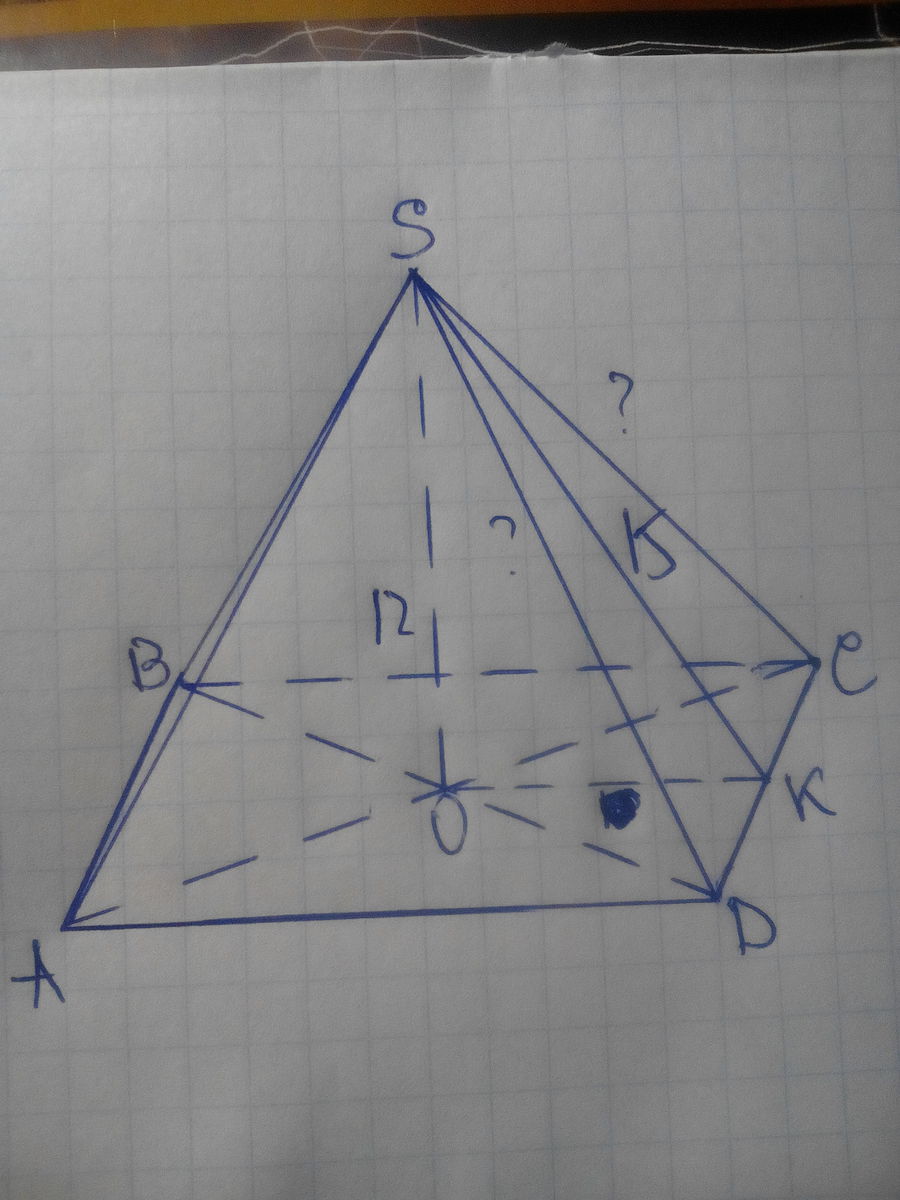
в правильной четырехугольной пирамиде высота равна 12 см а высота боковой грани - 15 см. найдите боковое ребро

с прямоугольного треугольника SKO(угол SOK=90°)
по т. Пифагора:
OK=√(15²-12²)=9 см

OD - радиус описанной окружности

сторона AD=2•OK=18 см

OD=(AD/2)/sin(180/n)=(AD/2)/sin(180/4)=9/sin45=9√2 см

С прямоугольного треугольника SDO(уголSOD=90°)
по т. Пифагора

SD²=SO²+OD²
SD=√(12²+(9√2)²)=√(144+162)=√306=3√34

Ответ: 3√34.