Решите уравнение Sin X * Cos X - 5 Sin^2 X = - 3 и найдите его корни, принадлежащие интервалу (-П/2 ; П)

Ответы

Ответ дал: Алкадиеныч

$sinxcosx-5sin^2x=-3$

$3cos^2x+sinxcosx-2sin^2x=0$ поделим на $cos^2xneq 0$

$-2tg^2x+tgx+3=0$

Тут очевидно подбираются корни по т Виета., это -1, и потом у нас при tg^2x есть -2, не забывает про нее.

$tgx=-1, and, tgx=1.5$

$x=-frac{pi }{4}+pi n ,and,x=arctg1.5+pi n$

n-целые

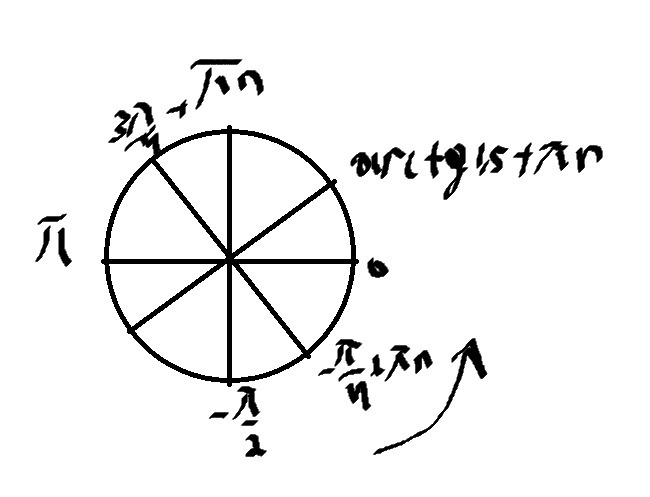
Б) Корни

$x=-frac{pi }{4},acrtg1.5, frac{3pi }{4}$

Приложения:

Похожие вопросы

Другие предметы

2 года назад

Английский язык

2 года назад

Химия

7 лет назад

Математика

7 лет назад

Физика

10 лет назад

Математика

10 лет назад

Математика

10 лет назад

География

10 лет назад