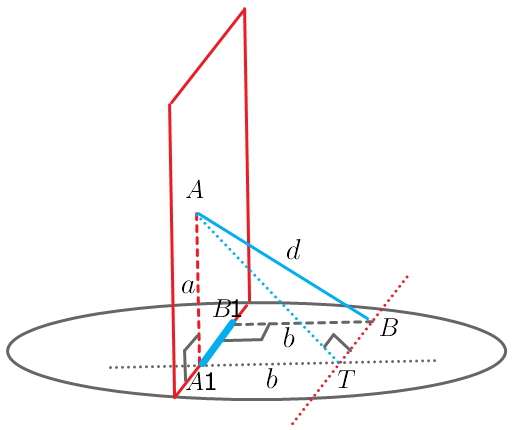
Точки А и В лежат в перпендикулярных плоскостях и соединены отрезком d ,перпендикуляры,проведенные с этих точек до линии пересечения равны а и б ,найти
расстояние между основаниями этих перпендикуляров.

в одной какой-нибудь плоскости 
через точку проведем прямую, параллельную линии пересечения плоскостей
и через проекцию другой точки проведем прямую, параллельную перпендикуляру из первой точки)))
получим прямоугольник ВВ1А1Т
А1Т = b
искомое расстояние А1В1 = ВТ
АТ² = a² + b²
A1T _|_ BT
AT _|_ BT (по теореме о трех перпендикулярах)))
ВТ² = d² - AT² = d² - a² - b²
BT = √(d² - a² - b²)