Катеты прямоугольного треугольника равны 8 и 15см. Чему равно расстояние от
вершины прямого угла до ближайшей точки вписанной в этот треугольник
окружности?
Ответы
Ответ дал:
19
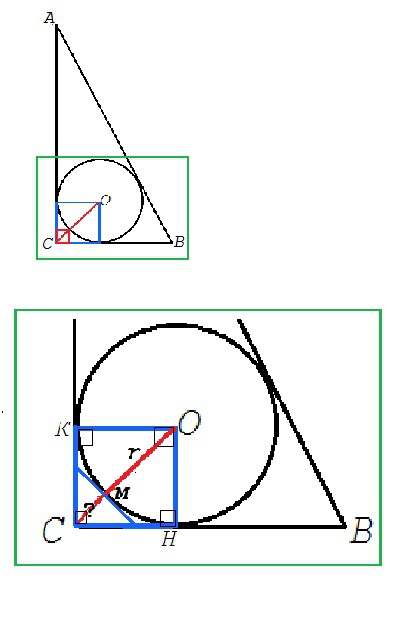
Искомое расстояние равно разности расстояния от вершины прямого угла до центра окружности и радиуса вписанной в этот треугольник окружности. Формула радиуса вписанной в прямоугольный треугольник окружности
r=(a+b-c):2 где а и b катеты, а с - гипотенуза.
Чтобы найти радиус, нужно знать гипотенузу. Она равна 17 см ( отношение сторон данного треугольника из Пифагоровых троек 8:15:17. Можно проверить по т.Пифагора)
r=(8+15-17):2=3 см
Радиус вписанной окружности перпендикулярен сторонам в точках касания.
ОН=ОК=3, четырехугольник ОМСК - квадрат.
Расстояние СО от прямого угла до центра равно диагонали d этого квадрата. d=3√2 см
Нет нужды доказывать, что расстояние измеряется перпендикуляром,
СМ ⊥ отрезку касательной в точке М, и М является ближайшей к вершине С точкой вписанной окружности.
CМ=СО-ОМ=3√2-3=3(√2-1) см
r=(a+b-c):2 где а и b катеты, а с - гипотенуза.
Чтобы найти радиус, нужно знать гипотенузу. Она равна 17 см ( отношение сторон данного треугольника из Пифагоровых троек 8:15:17. Можно проверить по т.Пифагора)
r=(8+15-17):2=3 см
Радиус вписанной окружности перпендикулярен сторонам в точках касания.
ОН=ОК=3, четырехугольник ОМСК - квадрат.
Расстояние СО от прямого угла до центра равно диагонали d этого квадрата. d=3√2 см
Нет нужды доказывать, что расстояние измеряется перпендикуляром,
СМ ⊥ отрезку касательной в точке М, и М является ближайшей к вершине С точкой вписанной окружности.
CМ=СО-ОМ=3√2-3=3(√2-1) см
Приложения:
Похожие вопросы
1 год назад
1 год назад
2 года назад
2 года назад
7 лет назад
8 лет назад