103 балла!
В треугольнике ABC: BM-медиана, точка K делит BM пополам. AK пересекает сторону BC в точке D. Найдите отношение площадей фигур: KDCM и AKM.

Приложения:
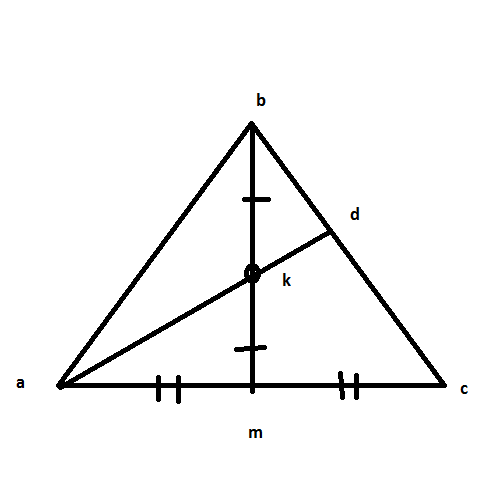
Не стоит отмечать лучшим ответ, скопированный с чужого решения задачи с другим условием, не подходящим к тому, что дано в задании.
Ответы
Ответ дал:
2
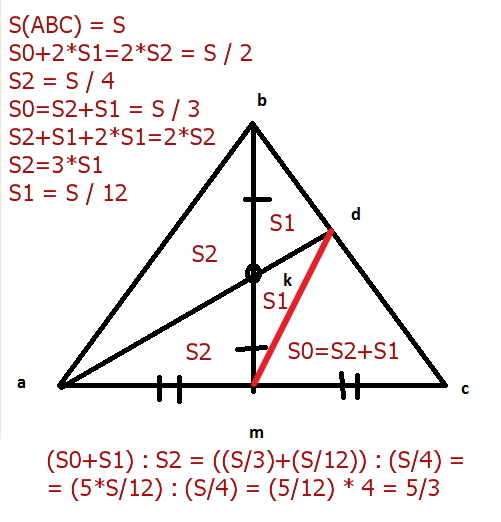
медиана делит треугольник на два равных по площади)))
отрезок DM тоже будет медианой для треугольника ADC...
чтобы найти отношение -- нужно постараться выразить все площади через что-либо общее, например, через площадь треугольника АВС)))
отрезок DM тоже будет медианой для треугольника ADC...
чтобы найти отношение -- нужно постараться выразить все площади через что-либо общее, например, через площадь треугольника АВС)))
Приложения:
Похожие вопросы
1 год назад
6 лет назад
8 лет назад
То есть ВС равна ВР+2ВР = 3ВР или ВС разделена точкой Р на части 1/3 и 2/3.
Итак, СР = ВС*2/3. Площадь треугольника АСР равна площади треугольника АВС минус площадь треугольника АВР. По известной формуле S=1/2*BC*h имеем площадь тр-ка АВС. Заметим, что у тр-ков АВС, АВР и АРС высота h, проведенная к основанию ВС (ВР,РС) одна и та ж