ПОМОГИТЕ ПОЖАЛУЙСТА ИССЛЕДОВАТЬ ФУНКЦИЮ И ПОСТРОИТЬ ГРАФИК:
y=1/(x²-3x).
Аноним:
Скину через 30 мин
хорошо
Ответы
Ответ дал:
1
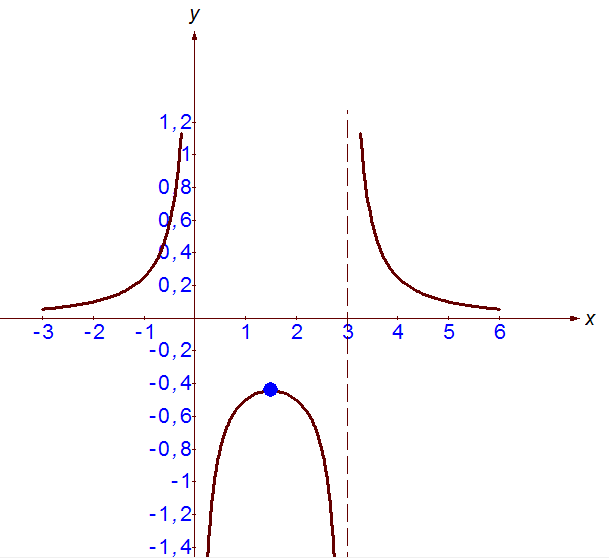
1. Область определения функции
2. Нечетность функции
Итак, функция ни четная ни нечетная.
3. Точки пересечения с осью Оу и Ох
3.1. С осью Ох (у=0)
Дробь, обращается в 0 тогда, когда числитель равно нулю
Точки пересечения с осью Ох нет
3.2. С осью Оу (х=0)
Точки пересечения с осью Оу нет
4. Критические точки, возрастание и убывание функции
Дробь будет 0 тогда, когда числитель равно нулю
__+__(0)___+__(1.5)___-___(3)__-___
Итак, Функция возрастает на промежутке (-∞;0) и (0;1.5), а убывает на промежутке (1.5;3) и (3;+∞). В точке х=1,5- функция имеет локальный максимум; (1.5;-4/9) - относительный максимум
5. Точки перегиба:
D<0, значит уравнение корней не имеет
Возможные точки перегиба: нет.
Вертикальные асимптоты (D(y)):
Наклонных асимптот нет.
Горизонтальные асимптоты: y=0
Приложения:
ОГРОМНОЕ СПАСИБО!!!)))
На здоровье!
Похожие вопросы
1 год назад
1 год назад
2 года назад
7 лет назад
8 лет назад