Предмет: Геометрия
Автор: Kotova10
Вопрос задан 10 лет назад

1Сторона РК и РМ треугольника РМК равны, PN его медиана. Найдите углы PHK и KPH, если угол МРК= 42 градуса 2Луч КС биссектриса угла DBK, а отрезок DK равен отрезку BK.Докажите, что треугольник KDC=треугольнику KBC 3 На основании NK равнобедренного треугольника NBK отложены отрезки NA=KC.Докажите что угол NBA=углу KBC 4В окружности с центром О проведены диаметры АС и хорда ВD, пересекающиеся в точке М, причем ВМ=DМ. угол ВАС=35 градусам. найдите угол ВАD

Ответы

Ответ дал: KuOV

Решение первых трех задач дано LopaAnt Хорошист

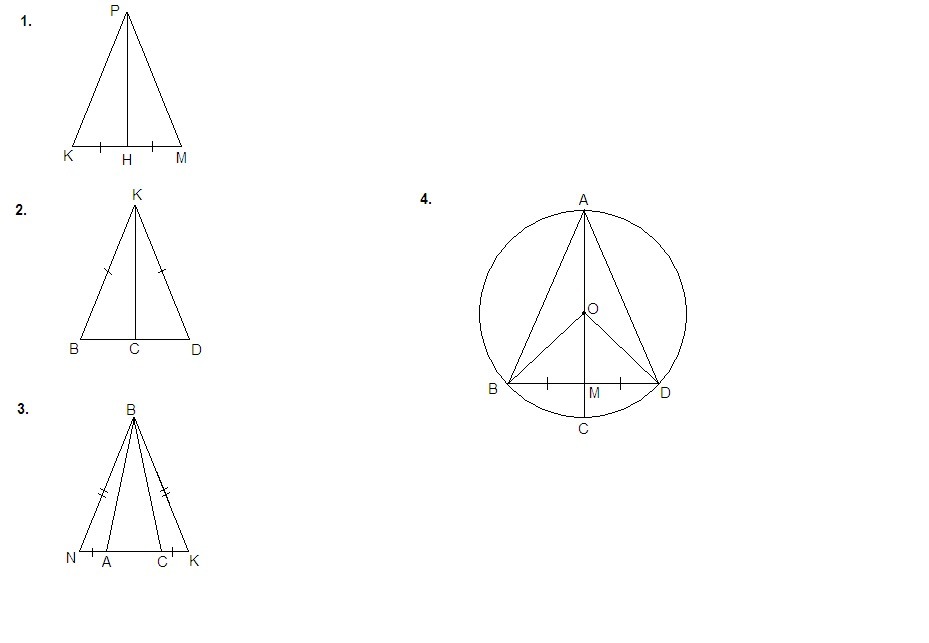
1. Стороны РК и РМ треугольника РМК равны, PН его медиана. Найдите углы PHK и KPH, если ∠МРК = 42°.

Треугольник равнобедренный, поэтому РН - медиана, высота, биссектрисса. =>

РHK = 90 гр., KPH = МРК/2 = 42/2 = 21.

2. Луч КС биссектриса угла DKВ, а отрезок DK равен отрезку BK. Докажите, что ΔKDC = ΔKBC.

Рассмотрим треугольник KDC и треугольник KBС;

DK = BK, ∠DKC = ∠СКВ - по условию.

КС - общая.

ΔKDC = ΔKBС по двум сторонам и углу между ними.

3. На основании NK равнобедренного треугольника NBK отложены отрезки NA = KC. Докажите, что ∠NBA = ∠KBC.
рассмотрим треугольники NBA и KBC. угол BNA и угол BKC равны как углы при основании равнобедренного треугольника. BN = BK, NA = KC - по условию. треугольники NBA и KBC равны по двум сторонам и углу между ними. из равенства треугольников следует равенство углов NBA и KBC.

4. В окружности с центром О проведены диаметры АС и хорда ВD, пересекающиеся в точке М, причем ВМ = DМ. ∠ВАС = 35°. Найдите угол ВАD.

Соединим точку О с концами хорды BD. OB = OD как радиусы окружности, значит ОМ - медиана и высота равнобедренного треугольника OBD.
То есть, AC⊥BD.
Тогда в треугольнике ABD АМ - медиана и высота, ⇒ ΔABD равнобедренный. Значит АМ еще и его биссектриса.
∠BAD = 2·∠BAC = 2·35° = 70°

Приложения: