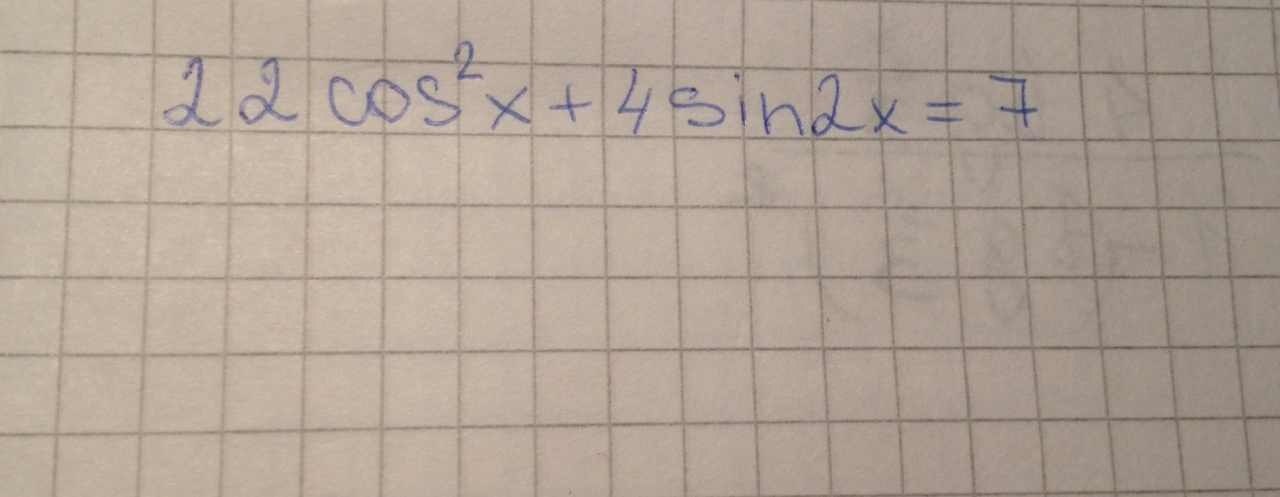Ответы
Ответ дал:
0
22cos^2x+4(2sinxcosx)=7(cos^2x+sin^2x)
22cos^2x+8sinxcosx=7cos^2x+7sin^2x
15cos^2x+8sinxcosx-7sin^2=0 /:cos^2
15+8tgx-7tg^2x=0
tgx=t
-7t^2+8t+15=0
7t^2-8t-15=0
D=64+420=484
t=8(+-)22
---------
14
t1=2
t2=1
tgx=1 tgx=2
x=arctg1+ПK x=arctg2+ПK
Ответ дал:
0
22cos^2x+4sin2x=7
22cos^2x+4sin2x=7(cos^2x+sin^2x)=o
22cos^2x+8sinx*cosx-7cos^2-7sin^2x=0
15cos^2x+8sinx*cosx-7sin^2x=0 /sin^2x
15ctg^2x+8ctgx-7=0
ctgx=t
15t^2+8t-7=0
Теперь находи дискреминант потом икс первое и второе и решай 2 простых уравнения
Похожие вопросы
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад