Помогите пожалуйста!!!Я не могу решить!!

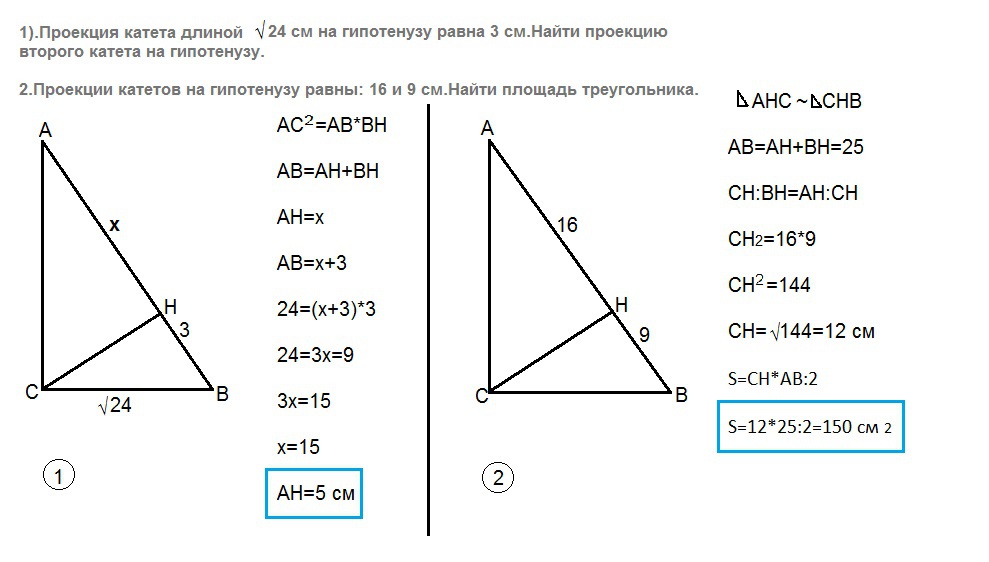
1.Проекция катета длиной корень из 24 см на гипотенузу равна 3 см.Найти проекцию второго катета на гипотенузу.
 Катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.
Гипотенуза АВ равна сумме проекций катетов 
АВ=АН+ВН
Пусть АН=х, тогда АВ=х+3
ВС²=АВ*ВН
24=(х+3)*3
24=3х+9⇒
х=5
АН=5
----------------
2.Проекции катетов на гипотенузу равны: 16 и 9 см.Найти площадь треугольника.
Площадь прямоугольного треугольника равна половине произведения высоты из прямого угла и гипотенузы. 
S=CН*АВ:2
 Высота, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу.
СН²=9*16=144
СН=√144=12 см
S=12*25:2=150 см²