В треугольнике АВС АВ=8 , ВС=7
, ВС=7 , .угол B = 120
, .угол B = 120
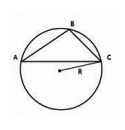
Найдите радиус R описанной окружности.
Приложения:
Ответы
Ответ дал:
8
S(ABC) = (1/2) * AB * BC * sin(ABC)
S(ABC) = AB*BC*CA / (4R)
CA² = AB² + BC² - 2*AB*BC*cos(ABC)
--------------------------------------------------------
S(ABC) = 8√3 * 7√3 * √3 / 4 = 42√3
CA² = 64*3 + 49*3 - 2*8*7*3*(-1/2)
CA² = 3*(113+56) = 3*13²
4R = 8√3 * 7√3 * 13√3 / (42√3)
4R = 8*7*3*13 / (2*3*7) = 4*13
R = 13
S(ABC) = AB*BC*CA / (4R)
CA² = AB² + BC² - 2*AB*BC*cos(ABC)
--------------------------------------------------------
S(ABC) = 8√3 * 7√3 * √3 / 4 = 42√3
CA² = 64*3 + 49*3 - 2*8*7*3*(-1/2)
CA² = 3*(113+56) = 3*13²
4R = 8√3 * 7√3 * 13√3 / (42√3)
4R = 8*7*3*13 / (2*3*7) = 4*13
R = 13
cmerti:
скажите, почему в этом треугольнике применяется теорема косинуса,если это не прямоугольный треугольник т.к. угол B=120
т.косинусов выполняется ДЛЯ ЛЮБОГО треугольника... это по определению косинус можно ВЫЧИСЛИТЬ как отношение прилежащего катета к гипотенузе))) а вообще понятие косинус --- шире --- это функция ЛЮБОГО угла, не только острого или тупого, но любого... например угол в 270 градусов ---для него вычислен косинус...
Похожие вопросы
1 год назад
1 год назад
1 год назад
6 лет назад