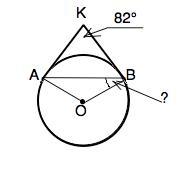
Касательные к окружности с центром O в точках A и B пересекаются под углом 82∘. Найдите угол ABO. Ответ дайте в градусах.

Ответ:41°

Объяснение: Пусть К – точка пересечения касательных.

Сумма углов четырехугольника 360°. Радиус, проведенный в точку касания, перпендикулярен касательной.  В четырехугольнике АКВО ∠КАО+∠КВО=2•90°,⇒

∠АОВ+∠АКВ=360°-2•90°=180°

∠АОВ=180°-82°=98°

АО=ВО - радиусы.

∆ АОВ - равнобедренный.

Из суммы углов треугольника ∠ВАО=∠АВО=(180°-98°):2=41°.