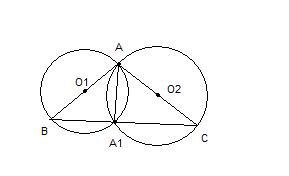
Две окружности с центрами в точках О1 и О2 пересекаются в точках А и А1, а отрезки АВ и АС - их диаметры. Найдите величины углов АА1В и АА1С и докажите, что точки В, А1 и С лежат на одной прямой.

Рассмотрим угол АА1В. Это вписанный угол в окружность с центром О1, который опирается на полуокружность АВ. Следовательно, он равен 90°. 
Рассмотрим угол АА1С. Это также вписанный угол в окружность с центром О2, который опирается на полуокружность АС. Следовательно, он тоже равен 90°.
<AA1B+<AA1C=90+90=180°, т.е. угол ВА1С - развернутый. Обе стороны развернутого угла лежат на одной прямой. Т.е. точки В, А1 и С лежат на одной прямой.