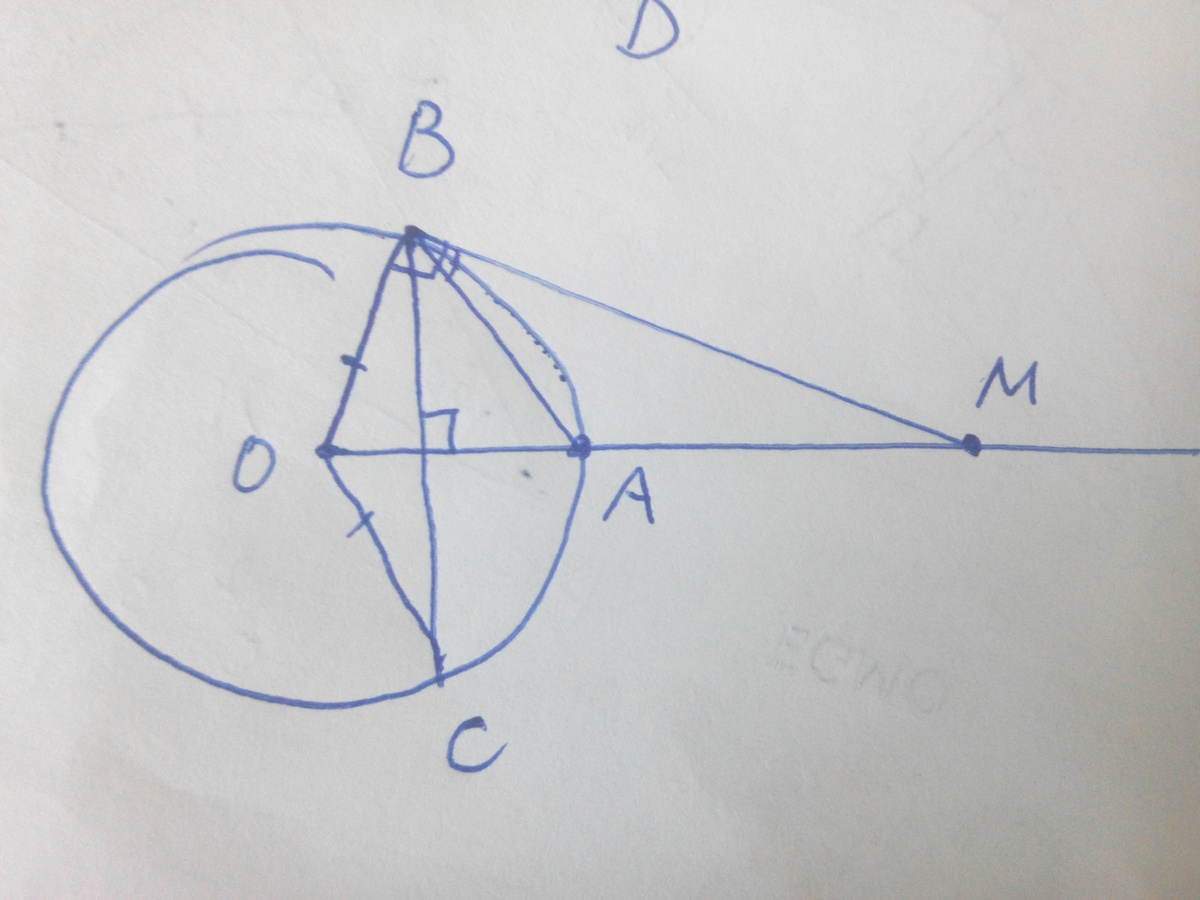
Радиус ОА окружности с центром О проходит через середину хорды ВС . Через точку В проведена касательная к окружности , пересекающая прмую ОА в точку М.
Докажите , что луч ВА - биссектриса угла СВМ
Рисунок обязателен.

∠MBA=∠BOA/2 как угол между касательной и хордой в точку касания.
Т.к. треугольник BOC равнобедренный, то OA⊥BC. Значит ∠OBC=90°-∠BOA. Значит ∠CBM=∠OBM-∠OBC=90°-(90°-∠BOA)=∠BOA. Итак, ∠MBA=∠CBM/2, т.е. BA - биссектриса ∠CBM.