геометрия( помогите пожалуйста Доказать подобие треугольников .
Приложения:
Andr1806:
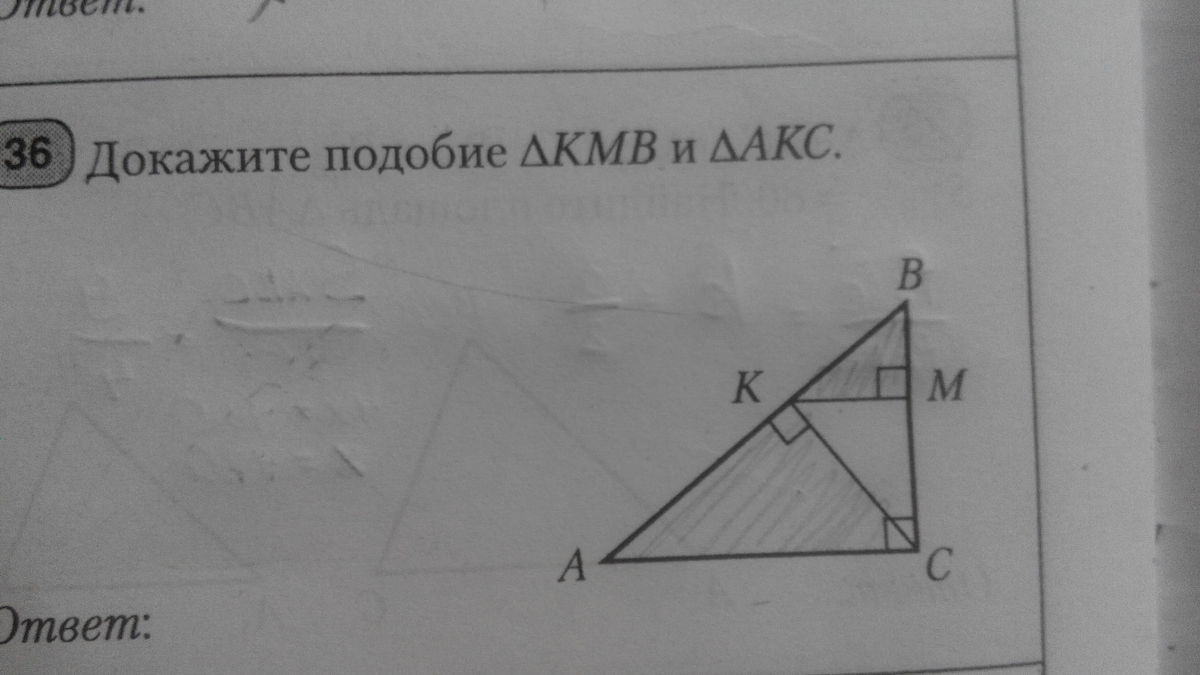
КМ и АС перпендикулярны ВС, значит они параллельны. Тогда <BKM=<KAC как соответственные при параллельных прямых КМ и АС и секущей АВ. Следовательно, прямоугольные треугольники КИВ и АКС подобны по острому углу.
Ответы
Ответ дал:
5
∠BKM=90°-∠B из треугольника KMB.
∠A=90°-∠B из треугольника ABC. Значит ∠BKM=∠A. Кроме того ∠AKC=∠KMB=90°. Итак, в треугольниках KMB и AKC по два угла равны, и, значит, они подобны.
∠A=90°-∠B из треугольника ABC. Значит ∠BKM=∠A. Кроме того ∠AKC=∠KMB=90°. Итак, в треугольниках KMB и AKC по два угла равны, и, значит, они подобны.
Похожие вопросы
1 год назад
1 год назад
1 год назад
1 год назад
6 лет назад