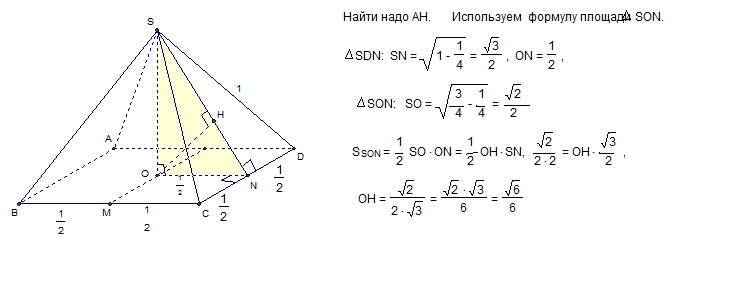
В правильной четырехуольной пирамиде SABCD, все ребра которой равны 1, найдите расстояние от середины ребра ВС до плоскости SCD.
Ответы
Ответ дал:
0
Чтобы найти расстояние от точки (М) до плоскости (SCD), можно через эту точку провести прямую MO, параллельную CD. Тогда эта прямая будет параллельна плоскости SCD. Потом из любой точки (О) этой прямой провести перпендикуляр (ОН) к плоскости - это и будет искомым расстоянием. Остальное решение во вложении. Кстати, координатный метод очень хорош в таких задачах. Жаль, что в школах так мало уделяют времени этому методу.
Приложения:
Похожие вопросы
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад