Найдите площадь равнобедренной трапеции, диагональ которой равна 10 и наклонена к основанию под углом 60 градусов. С подробным решением, пожалуйста.
Ответы
Ответ дал:
13
1) Площадь трапеции равна:

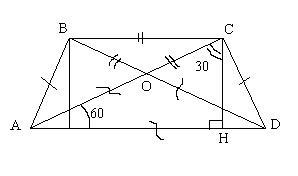
2) Рассмотрим прямоугольный треугольник ACH:
Угол CAH=60, значит угол ACH=30.
Катет AH лежит против угла в 30 градусов, значит он в 2 раза меньше гипотенузы:

По теореме Пифагора:

3) Проведем вторую диагональ BD=AC (т.к. трапеция равнобедренная).
Трапеция равнобедренная, значит углы при основаниях равны:
угол BAD=угол CDA, угол ABC=угол BCD
угол CAD=угол BDA=60, значит угол AOD=60 => треугольник AOD - равносторонний (все углы по 60 градусов): AO=OD=AD
Аналогично с треугольником BOC: BO=OC=BC
4) AC=AO+OC=10
BD=BO+OD=10
Следовательно: AD+BC=10
5)
2) Рассмотрим прямоугольный треугольник ACH:
Угол CAH=60, значит угол ACH=30.
Катет AH лежит против угла в 30 градусов, значит он в 2 раза меньше гипотенузы:
По теореме Пифагора:
3) Проведем вторую диагональ BD=AC (т.к. трапеция равнобедренная).
Трапеция равнобедренная, значит углы при основаниях равны:
угол BAD=угол CDA, угол ABC=угол BCD
угол CAD=угол BDA=60, значит угол AOD=60 => треугольник AOD - равносторонний (все углы по 60 градусов): AO=OD=AD
Аналогично с треугольником BOC: BO=OC=BC
4) AC=AO+OC=10
BD=BO+OD=10
Следовательно: AD+BC=10
5)
Приложения:
Похожие вопросы
1 год назад
2 года назад
2 года назад
6 лет назад
6 лет назад
8 лет назад