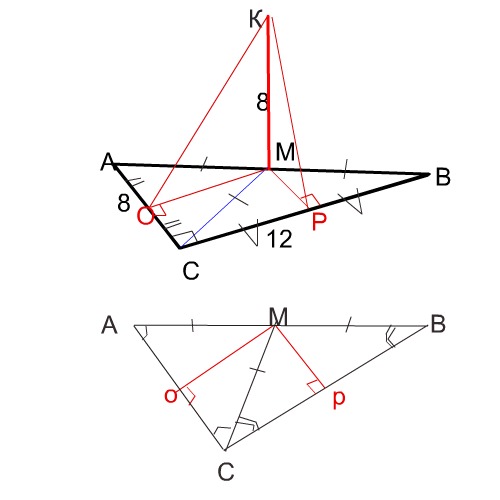
Помогите пожалуйста с задачей по теме прямые и плоскости в пространстве Катеты прямоугольного треугольника равны 8см и 12см Из точки M которая делит гипотенузу пополам к плоскости этого треугольника проведён перпендикуляр KM равный 8см Найти расстояние точки K до каждого катета

СМ- медиана прямоугольного треугольника и равна половине его гипотенузы.

Через медиану в треугольнике образовались два равнобедренных треугольника
Δ АМС и Δ СМВ, высоты МО  и МР которых являются проекциями наклонных КО и  КР. Эти наклонные и есть расстояние от К до катетов треугольника.

Гипотенузу АВ найдем по теореме Пифагора:
АВ²=АВ²+СВ²=208

медиана МС=АМ=МВ

МО²=(АВ:2)²-АО²

МО²=(√208:2)²-4²

МО²= 208:4 -16=36
МО=6

Расстояние от К до О находим по теореме Пифагора, хотя и без вычислений ясно,что гипотенуза прямоугольного треугольника с катетами 6 и 8 равна 10.
КО=10

Проекцию МР наклонной КР найдем по теореме Пифагора:

МР²=(АВ:2)²-ВР²

МР²=(√208:2)²-6²
МР²=208:4 -36=16
МР=4

Расстояние от К до Р находим по теореме Пифагора:
КР²=КМ²+РМ²
КР²=64+16=80

КР=4√5