одна з діагоналей ромба дорівнює його стороні . знайдіть гострий кут ромба

Дано :

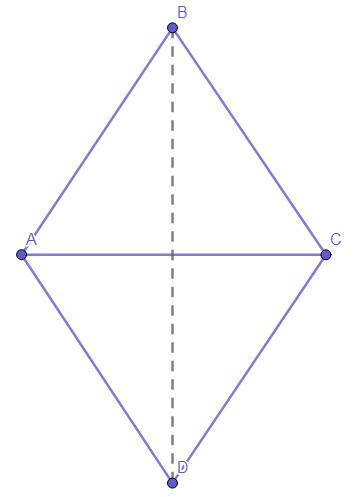
Четырёхугольник ABCD - ромб.

Отрезки АС и BD - диагонали.

АС = АВ.

Найти :

Острый угол = ?

Решение :

Ромб - это параллелограмм, у которого все стороны равны.

Поэтому -

АВ = ВС = CD = AD.

Рассмотрим ΔАВС.

АС = АВ = ВС.

Следовательно, ΔАВС - равносторонний (по определению равностороннего треугольника).

• Каждый угол равностороннего треугольника равен по 60°.

Отсюда -

∠ВАС = ∠В = ∠ВСА = 60°.

• Диагональ ромба является биссектрисой его угла.

То есть -

∠А = 60°*2 = 120°.

• Противоположные углы параллелограмма равны.

Следовательно -

∠В = ∠D = 60°

∠А = ∠С = 120°.

Отсюда острый угол ромба = 60°.

Ответ :

60°.