в правильной четырёхугольной пирмаиде сторона основания равна 12, апофема пирамиды равна 10. Найдите объём вписанного шара.

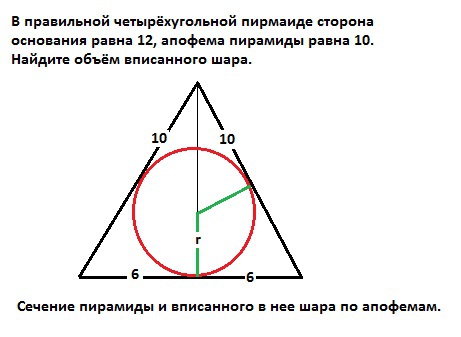
Вписанный в правильную пирамиду шар касается основания пирамиды (в его центре и апофем пирамиды. То есть в сечении пирамиды по ее апофемам мы имеем равнобедренный треугольник со сторонами, равными апофкмам и основанием, равным стороне квадрата (основания). В этот треугольник вписана окружность (сечение шара).
Есть формула радиуса вписанной в треугольник окружности: r=S/p, где S- площадь треугольника, а р - его полупериметр.
Найдем высоту пирамиды по Пифагору: √(10²-6²)=8  (10 - апофема, 6 - половина стороны квадрата). Тогда площадь треугольника равна S=8*6=48. Тогда радиус вписанной в треугольник окружности равен r=S/p= 48/16 = 3. Это и есть радиус вписанного в пирамиду  шара.
Второй вариант: по формуле радиуса вписанной в равнобедренный  треугольник окружности: r=(b/2)*√[(2a-b)/(2a+b)].
В нашем случае: r=6*√(1/4) = 3.
Объем шара находим по формуле: V=(4/3)*π*r³ =36π.
Ответ V = 36π.