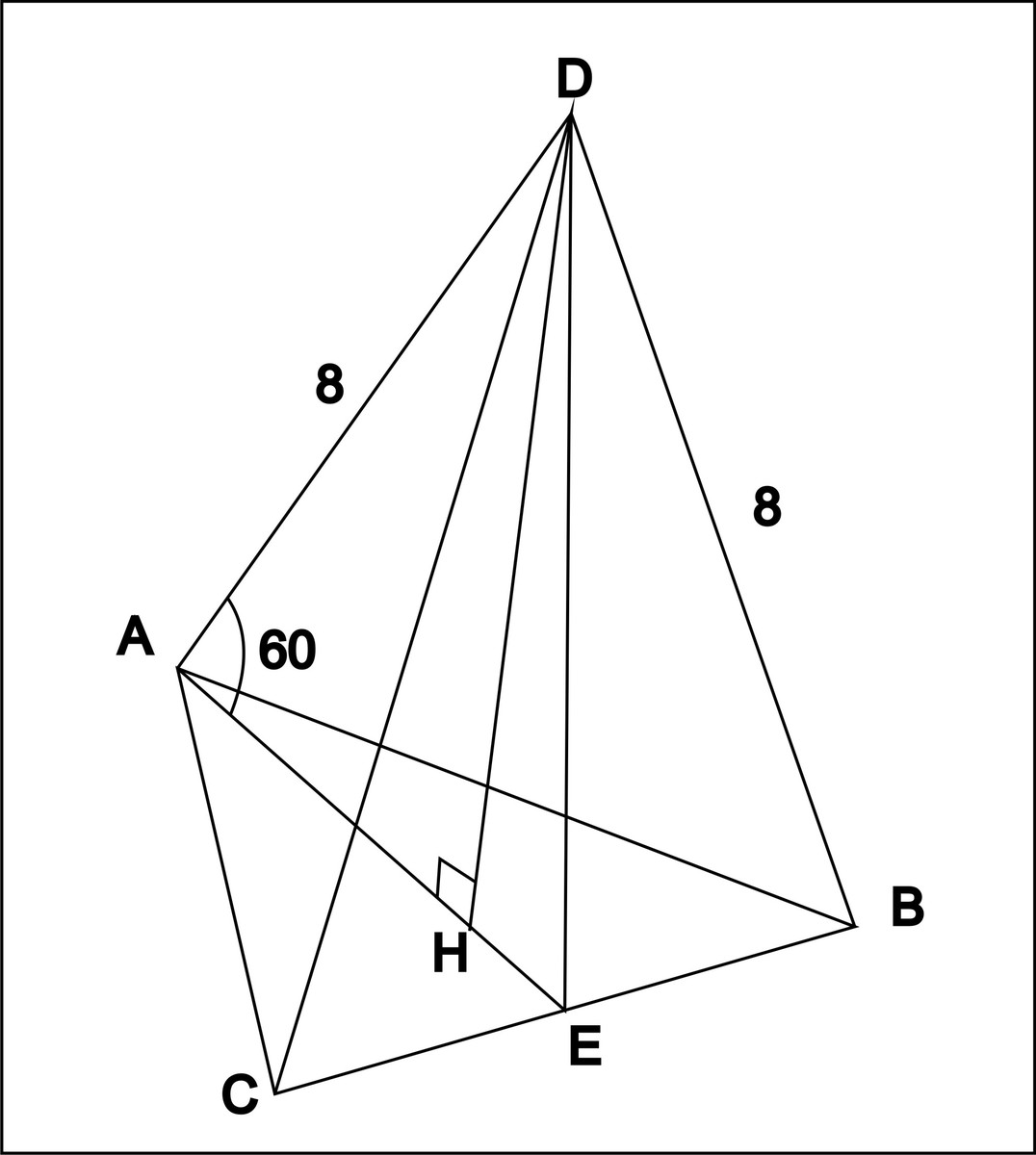
Боковое ребро правильной треугольной пирамиды равно 8 см и составляет с плоскостью основыния угол 60.Найдите площадь полной поверхности пирамиды.Помогите!

AH=AD·cos60=8/2=4
AE=(3/2)AH=6
тк треугольник АВС равносторонний то угол САЕ=30
AC=AE/cos30=6/(√3/2)=12/√3=CB
CE=(1/2)CB
DE²=DC²-CE²
DE=2√13
S(боковой повехности)=3·DE·(1/2)·CB=(36√13)/√3
S(основания)=(1/2)·AE·CB=36/√3
S(всей поверхности)=(36(√13+1))/√3