Помогите пожалуйста!!! Ребро правильного тетраэдра DABC равно а. Постройте сечение тетраэдра, проходящее через середину ребра DA параллельно плоскости DBC и найдите площадь сечения.

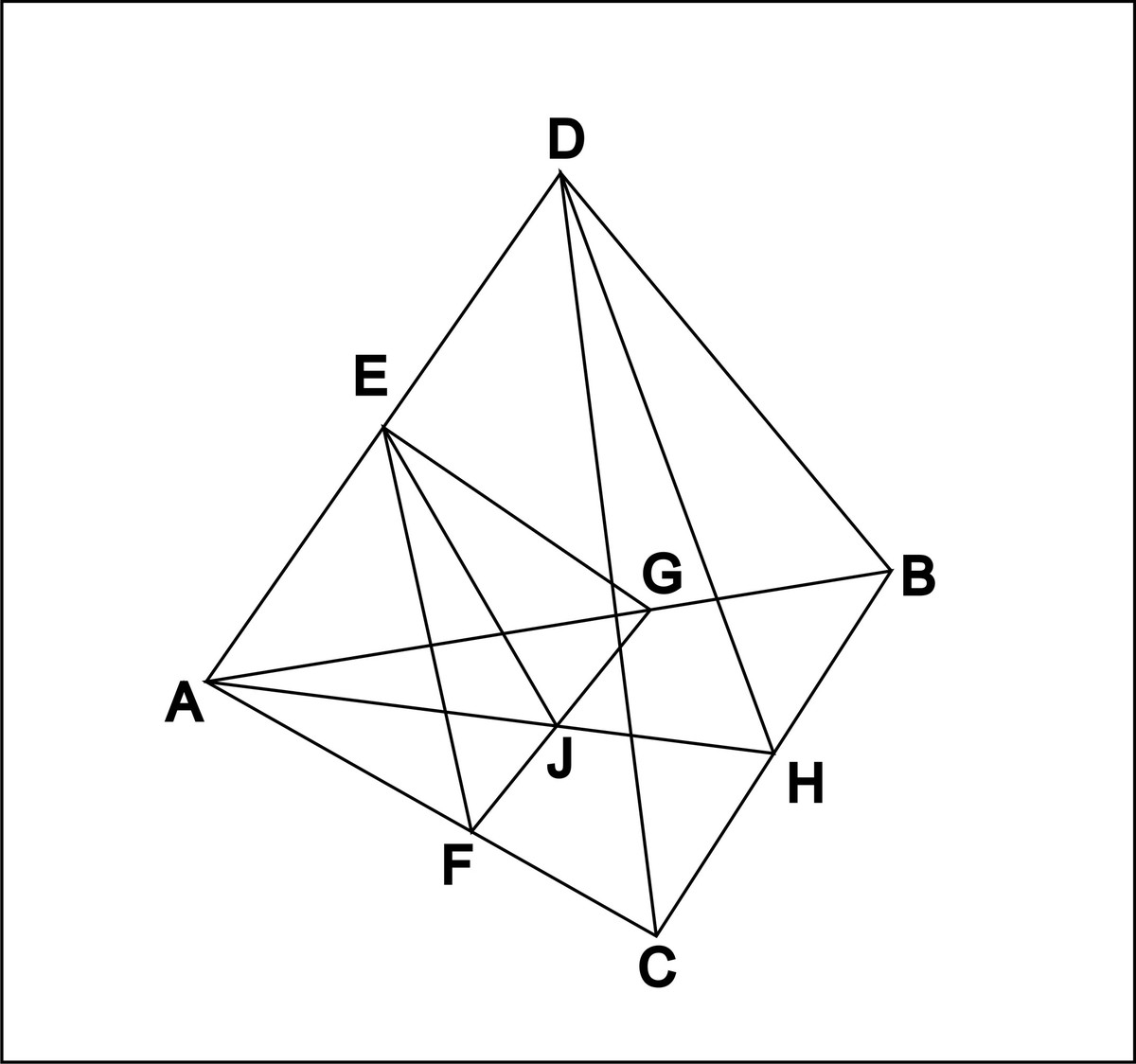
EGF - данное сечение
по скольку плоскости DBC и EGF параллельны то они отсекают от плоскости ADC параллельные прямые
EF|| DC
значит по теореме Фалеса
AE/ED=AF/FC=1
лоскости DBC и EGF параллельны то они отсекают от плоскости ADB параллельные прямые
EG|| DB
значит по теореме Фалеса
AE/ED=AG/GB=1
EF=DC/2=a/2=FG=EG
FJ=FG/2=a/4
EJ²=EF²-FJ²
EJ=(a√3)/4
S=FG·(1/2)·EJ=(a²√3)/16