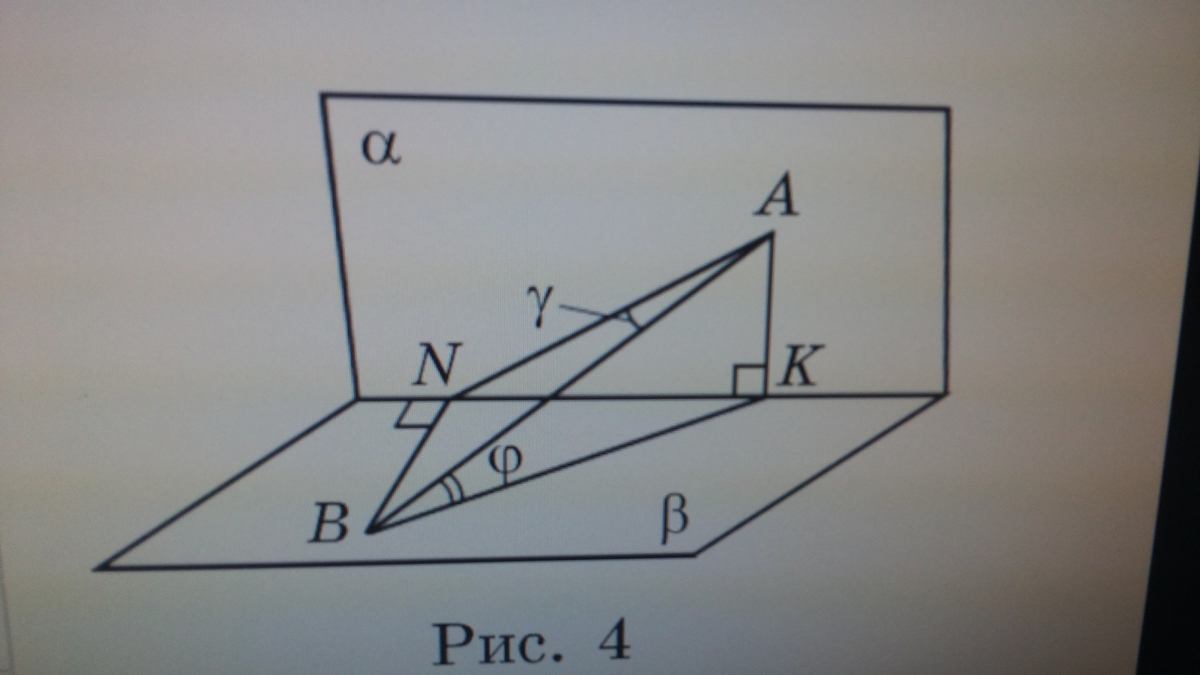
Плоскости α и β образуют прямой двугранный угол с прямой NK.Расстояние от прямой NK до точки А отрезка АВ в два раза больше,чем до точки В,найти отношение
угла NAB к углу АВК.
Приложения:
Ответы
Ответ дал:
1
АК = 2*NB - по условию
sin(NAB)=NB / AB
sin(ABK)=AK / AB
sin(NAB) / sin(ABK) =NB / AK = NB / (2*NB) = 1/2
sin(NAB) / sin(ABK) = 1/2 - это ответ
sin(NAB)=NB / AB
sin(ABK)=AK / AB
sin(NAB) / sin(ABK) =NB / AK = NB / (2*NB) = 1/2
sin(NAB) / sin(ABK) = 1/2 - это ответ
IUV:
так как по-Вашему это это не решение, то никто не мешает Вам предоставить свое РЕШЕНИЕ
ничего плохого не сказал , нужно доказать(если это так) что невозможно по этим данным определить требуемое ; иначе несерьезно
Вы же понимаете, что если получилось жесткое соотношение между синусами углов и так как углы могут изменяться, то для произвольного угла гамма и угла вета не может быть найдено отношение углов
хотя бы потому что синус - функция нелинейная
хотя бы потому что синус - функция нелинейная
я не вижу оснований сомневаться в отношении синусов
хотя бы потому что синус - функция нелинейная _аргумент
тут никаких других ответов быть не может, линейная она или нет...
спасибо за высказанное мнение !
ну, sin(γ)/sin(φ) = 1/2 устанавливается, а что тут еще можно получить? Не, может быть у кого-то есть волшебная палочка?
Хм.. Так же вчера решала, т.к. такое решение первым приходит в голову. Поискала, чтобы обосновать равенство отношения углов и их синусов, в теоремах - не нашла. Проверила на углах 30 и 60 градусов. Казалось бы, отношения углов и их синусов должны быть одинаковы, 1/2, но это не так...Возможно, ошибка в условии, и нужно было узнать отношение синусов. Тогда не возникает никаких вопросов. А ошибки в заданиях бывают сплошь и рядом...
..Возможно, ошибка в условии, и нужно узнать отношение синусов. Тогда не возникает никаких вопросов. А ошибки в заданиях бывают сплошь и рядом.
Похожие вопросы
1 год назад
1 год назад
1 год назад
6 лет назад
6 лет назад