Даю 100 баллов!
Постройте график функции y= 2,5*lхl-1 / lхl-2,5х^2 При каких значениях K прямая y=kx имеет с графиком ни одной общей точки

Аноним: :D

Аноним: У меня ответ верный?

Flex243: нет(

Flex243: ответ : 0, 6,25; -6,25

Flex243: ку ку

Flex243: где вы

Аноним: 2,5 тоже не имеет ни одну точку

Flex243: кому давать лучшее реш?))

Аноним: Коту)

Аноним: Решать тебе :D Чье понятнее и больше нравится. :З

Ответы

Ответ дал: Аноним

$y= \frac{2.5|x|-1}{|x|-2.5x^2} = \left \{ {{ -\frac{1}{x},\,\,\,\,if\,\,\,x\ \textgreater \ 0 } \atop { \frac{1}{x} ,\,\,\,\,if\,\,\,x\ \textless \ 0}} \right.$

ОДЗ: $x(x-2.5)\ne 0\\ x\ne 0\\ x\ne\pm 2/5$

При k=0 не имеет ни одной общей точки

$y( \frac{2}{5} )= \frac{1}{\frac{2}{5}} = \frac{5}{2} \\ \frac{5}{2} =\frac{2}{5}k \\ k=6.25 \\ y(-\frac{2}{5})= \frac{5}{2} \\ \frac{5}{2} =-\frac{2}{5}k\\ k=-6.25$

Приложения:

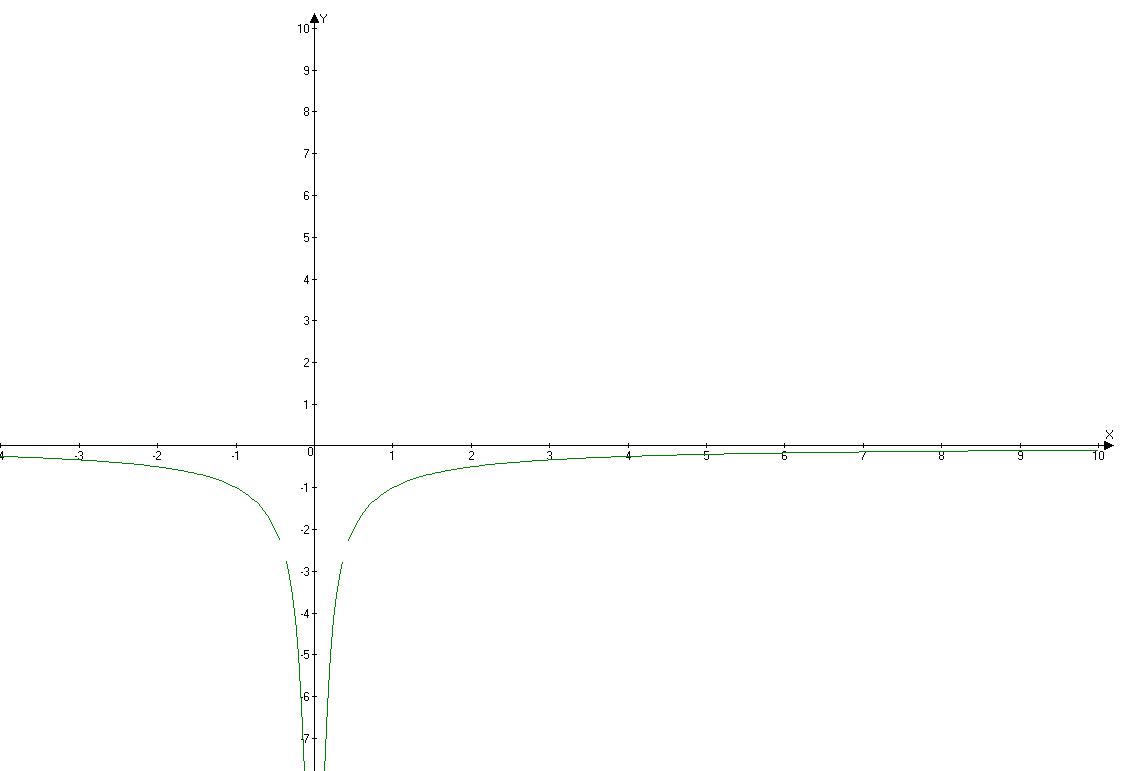
Аноним: Добавил график

Flex243: не

Аноним: что не так?)

Flex243: ответ : 0, 6,25; -6,25

Аноним: Бесит почему ±6.25 если (2.5)²=6.25

Аноним: А хотя есть

Аноним: Чет у тебя не то.

Аноним: С ОДЗ проблемы.

Аноним: ай да

Ответ дал: Аноним

$y=\frac{2,5|x|-1}{|x|-2,5x^2}$

ОДЗ: $|x|-2,5x^2 \neq 0$
$x(1-2,5x) \neq 0$
$x \neq 0,x \neq \frac{2}5$
$x(-1-2,5x) \neq 0$
$x \neq 0,x \neq -\frac{2}5$

Итого, ОДЗ: $x \neq 0,x \neq \frac{2}5,x \neq -\frac{2}5$

$1)x \geq 0$

$y=\frac{2,5x-1}{x-2,5x^2}=\frac{2,5x-1}{x(1-2,5x)}=-\frac{2,5x-1}{x(2,5x-1)}=-\frac{1}x$

$2)x\ \textless \ 0$
$y=\frac{-2,5x-1}{-x-2,5x^2}=\frac{2,5x+1}{x(1+2,5x)}=-\frac{2,5x+1}{x(2,5x+1)}=\frac{1}x$

График функции выглядит так: (см. вложения)

При таком расположении графиков возможно только три положения прямых y=kx, при котором она не имеет с графиком ни одной общей точки.

1. Эта прямая y=0, => k=0.
2. Эта прямая, проходящая через "выколотые точки" $x=\frac{2}5,x=-\frac{2}5$
$y(\frac{2}5)=\frac{5}2$
$y(-\frac{2}5)=\frac{5}2$
$y=kx=\ \textgreater \ \frac{5}2=\frac{2}5k=\ \textgreater \ k=\frac{25}{4}=6,25$
$y=kx=\ \textgreater \ \frac{5}2=-\frac{2}5k=\ \textgreater \ k=-\frac{25}{4}=-6,25$
Ответ: $k=б6,25,k=0$

Приложения: