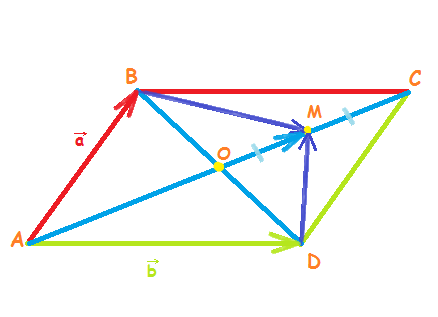
В параллелограмме ABCD: вектор AB=a, AD=b, точка О - пересечение диагоналей. М лежит на середине ОС. Выразите через a и b сумму: BM+DM.
Просьба с рисунком и поподробней.
Ответы
Ответ дал:
0
Диагонали при пересечении делятся пополам, значит АМ=3(a+b)/4.
По правилу треугольника,
BM=AM-AB;
DM=AM-AD.
Подставляем значения AM, AB и AD:
BM=3(a+b)/4-а=(3b-a)/4;
DM=3(a+b)/4-b=(3a-b)/4.
И наконец,
BM+DM=(3b-a)/4+(3a-b)/4=(a+b)/2.
(все это, конечно, векторы, но стрелочку над буквами писать не могу)
Приложения:
Похожие вопросы
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад
10 лет назад