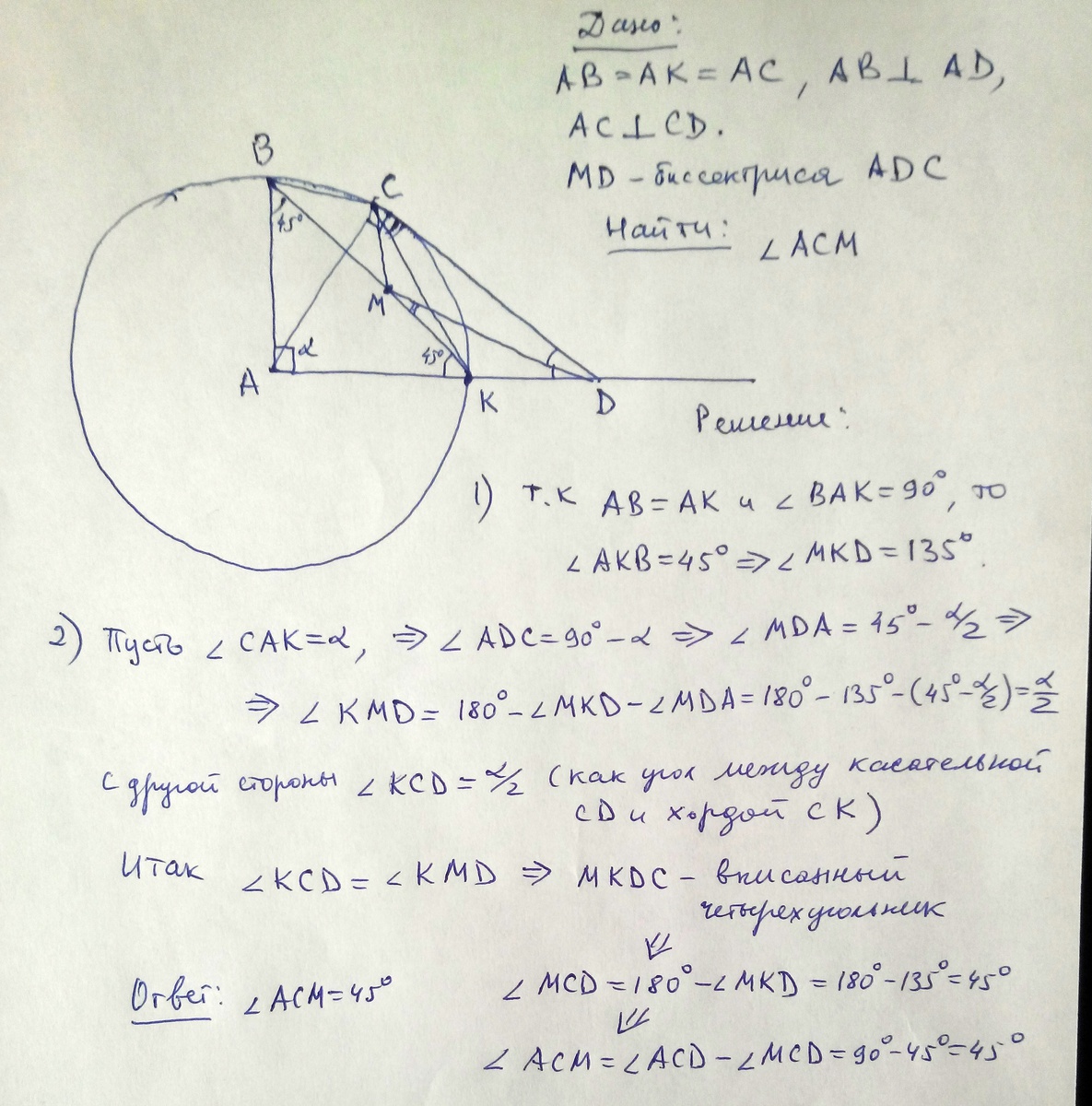
В четырёхугольнике ABCD сторона AB равна диагонали AC и перпендикулярна стороне AD, а диагональ AC перпендикулярна стороне CD. На стороне AD взята такая точка K, что AC=AK. Биссектриса угла ADC пересекает BK в точке M. Найдите угол ACM.

Denik777: Углы КСD и КМD равны и оприаются на общий отрезок KD, Такое может быть только, если вокруг МКДС можно описать окружность. (равные углы опираются на одну дугу). Ну или вспомнить, что геометрическое место вершин равных углов, опирающихся на один отрезок есть окружность.