параллельные прямые a и b пересечены двумя параллельными секущими АВ и CD, причем точки А и С принадлежат прямой а, а точки B и D - прямой b. докажите что АВ=CD
P.S. если можно с чертежом пожалуйста:)
Ответы
Ответ дал:
11
Две пары пересекающихся параллельных прямых отсекают четырехугольник ABCD, противоположные стороны которого попарно параллельны. т.к. принадлежат параллельным прямым.
⇒ АВСD- параллелограмм.
В параллелограмме противоположные стороны равны.
АВ и СD - противоположные стороны параллелограмма. ⇒ они равны.
--------
2.
В получившемся четырехугольнике соединим А и D. Треугольники АСD и имеют равные накрестлежащие углы при пересечении параллельных прямых а и b секущей AD, и той же секущей при пересечении параллельных прямых AB и CD, а сторона AD- общая.
Второй признак равенства треугольников. Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
⇒АВ=CD
⇒ АВСD- параллелограмм.
В параллелограмме противоположные стороны равны.
АВ и СD - противоположные стороны параллелограмма. ⇒ они равны.
--------
2.
В получившемся четырехугольнике соединим А и D. Треугольники АСD и имеют равные накрестлежащие углы при пересечении параллельных прямых а и b секущей AD, и той же секущей при пересечении параллельных прямых AB и CD, а сторона AD- общая.
Второй признак равенства треугольников. Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
⇒АВ=CD
Приложения:
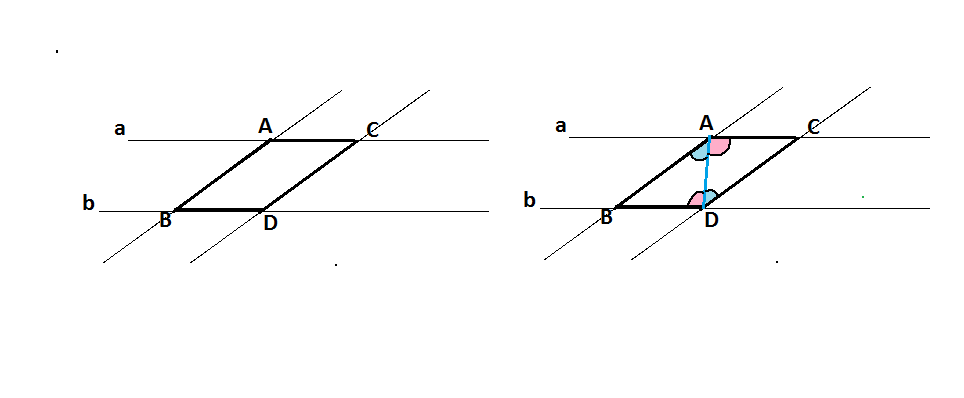
Похожие вопросы
1 год назад
1 год назад
1 год назад
8 лет назад
8 лет назад