Вершина второй параболы в уравнениях с модулем.
Пожалуйста, объясните, как найти координаты вершины второй параболы в уравнениях типа:
y = |x| * (x + 1) - 6x
y = 4|x + 6| - x² - 11x - 30
Я могу найти только координаты первой вершины, вот мой алгоритм на примере второго уравнения.
Записываю уравнение без знака модуля (вот тут ещё получается, что я как бы открываю скобки)
y = 4x + 24 - x² - 11x - 30
Привожу к общему виду
y = -x² - 7x - 6
Вместо y подставляю 0 и домножаю на -1
x² + 7x + 6 = 0
Корни уравнения: -1 и -6, полусумма корней (-3.5) - это X вершины первой параболы
Подставляю X в уравнение, приведённое к общему виду, и получаю Y вершины первой параболы (6.25).
А как вычислить координаты вершины второй параболы?
Ответы
Ответ дал:
0
По-моему так. Надеюсь, я вам помогла. Удачи вам
Приложения:
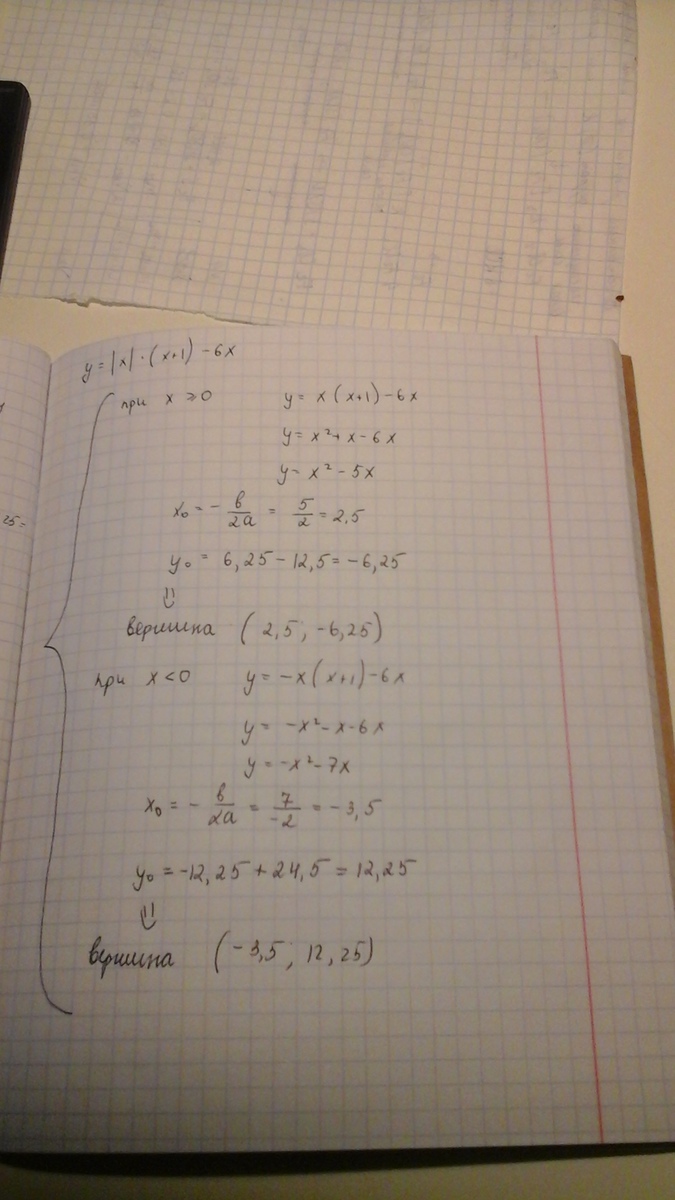
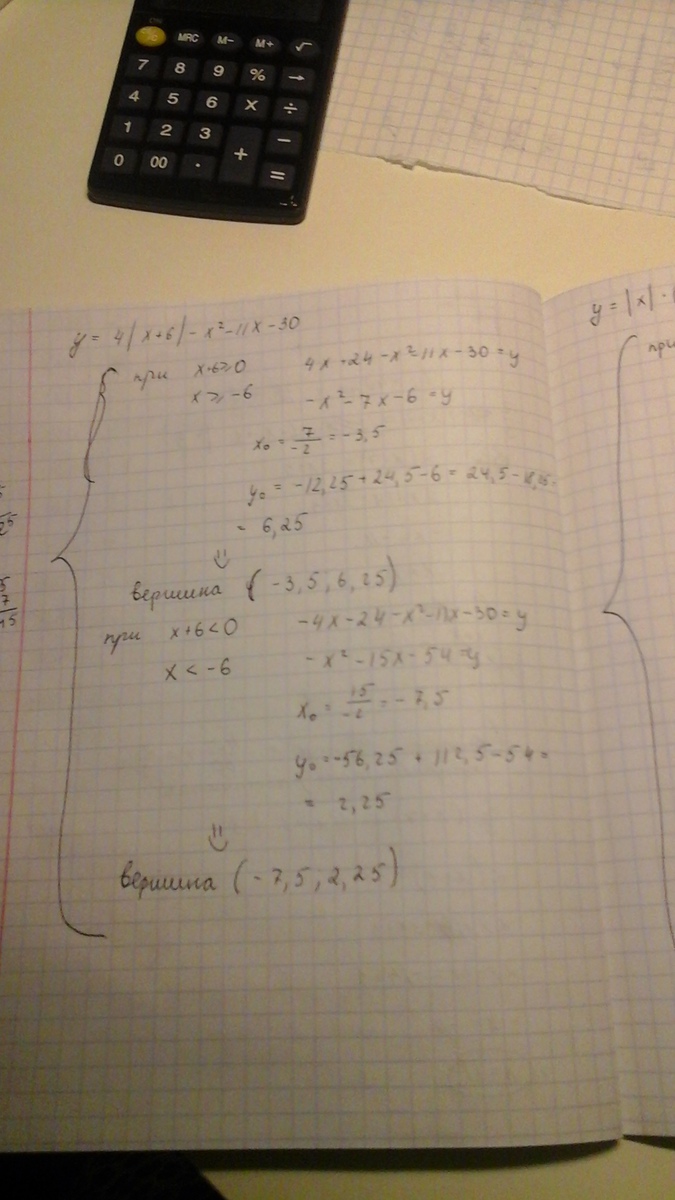
Похожие вопросы
1 год назад
1 год назад
1 год назад
1 год назад
6 лет назад
6 лет назад
8 лет назад