Диагонали трапеции ABCD с основаниями AB и CD пересекаются в точке О. Найдите: AO/OC и BO/OD, если AB=a, DC=b. решить со всеми рисунками

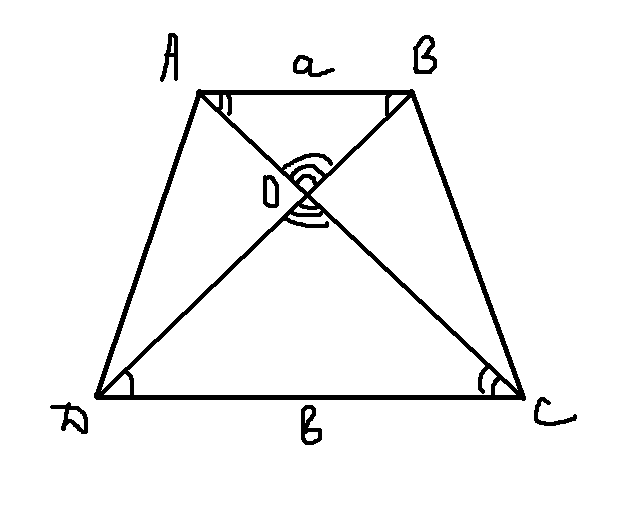
Рассм. тр. AOB и тр. DOC

- угол OAB = углу OCD (накрест лежащие, AB||DC, секущая AC)

- угол ABO = углу ODC (накрест лежащие, AB||DC, секущая BD)

- угол AOB = углу DOC (вертикальные углы)

Значит треугольники подобны, отсюда:

AB/DC=AO/OC=OB/OD

AB/DC=a/b ⇒ AO/OC=OB/OD=a/b

AO/OC=OB/OD=a/b