Предмет: Алгебра
Автор: ТатьянаRus
Вопрос задан 2 года назад

Найти неопределенный интеграл,упростив выражение,используя формулы тригонометрии(с подробным решением)

Приложения:

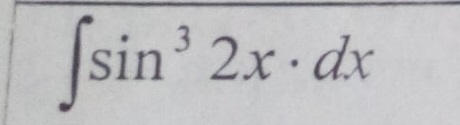
Ответы

Ответ дал: mymurkin

$\int\limits {sin^22xsin2x} \, dx = \int\limits- \frac{1}{2} (1-cos^22x) \, dcos2x|=|cos2x=t| =-1/2\int\limits {(1-t^2)} \, dt=-1/2t+1/2*1/3t^3=-1/2t+1/6t^3=- \frac{1}{2}cos2x+ \frac{1}{6}cos^32x$ +C
$f'(x)dx=d(f(x))$
sin2xdx=-1/2dcos2x

ТатьянаRus: откуда там 1/6 получилась?и что значит dcos?

Похожие вопросы

Русский язык

1 год назад

ПОМОГИТЕ СРОЧНО!!!ДАМ МАКСИМАЛЬНЫЙ БАЛЛ!) составить и записать диалог(8реплик) с междометиями и звукоподражательными словами,выделив их в тексте

Українська мова

1 год назад

Помогите пожайлуста !Провідміняйте числівники: 67246; 982583

Английский язык

1 год назад

Помогите написать личное письмо пожалуйста

Алгебра

1 год назад

помогите с 5 пожалуйста

Биология

6 лет назад

О каком критерии вида идёт речь? Чёрная ворона обитает в Западной Европе ,а серая ворона- в Восточной Европе и Западной Сибири.Помогите пожалуйста,срочно !!!!!

Українська мова

6 лет назад

чому мені подобається шахи.Творче завдання.3 предложения нужно Срочно нужно

Математика

8 лет назад

решите пожалуйстааа 2х+5/х²+х - 2/х=3х/х+1

Биология

8 лет назад

кроссворд на тему растения и животные гор .Минимум 10 слов .