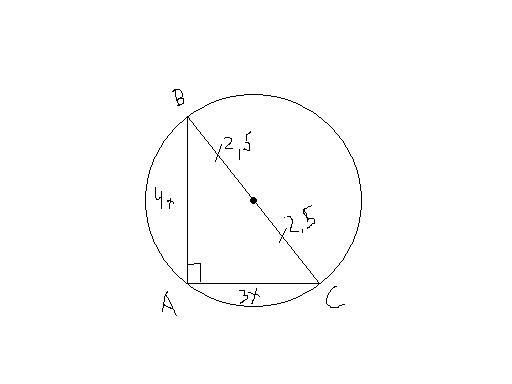
Около прямоугольного треугольника описана окружность радиуса 2,5 см. Найдите периметр и площадь этого треугольника, если его катеты относятся как 3:4
Ответы
Ответ дал:
31
Во вписанном прямоугольном треугольнике, центр окружности совпадает с серединой гипотенузы. Т.е из рисунка гипотенуза равна 5, т.к. радиус=2.5.
Т. к катеты относятся как 3 к 4 , то можно обозначить АВ=4*х, АС=3*х. Тогда по теореме пифагора имеем:
BC²=AC²+AB² подставим и решим
5=√((4*x)²+(3*x)²)
Х=1
АВ=4*1=4
АС=3*1=3
Периметр равен: 5+4+3=12
Площадь равна половине произведения катетов т.е
S=(4*3)/2=6
Т. к катеты относятся как 3 к 4 , то можно обозначить АВ=4*х, АС=3*х. Тогда по теореме пифагора имеем:
BC²=AC²+AB² подставим и решим
5=√((4*x)²+(3*x)²)
Х=1
АВ=4*1=4
АС=3*1=3
Периметр равен: 5+4+3=12
Площадь равна половине произведения катетов т.е
S=(4*3)/2=6
Приложения:
Похожие вопросы
1 год назад
1 год назад
2 года назад
2 года назад
6 лет назад
6 лет назад