Помогите с задачей по геометрии (из школы)
Периметр равнобедренного треугольника относится к его основанию как 8:3 .Найдите отношение радиусов вписанной и описанной окружности.
Ответы
Ответ дал:
1
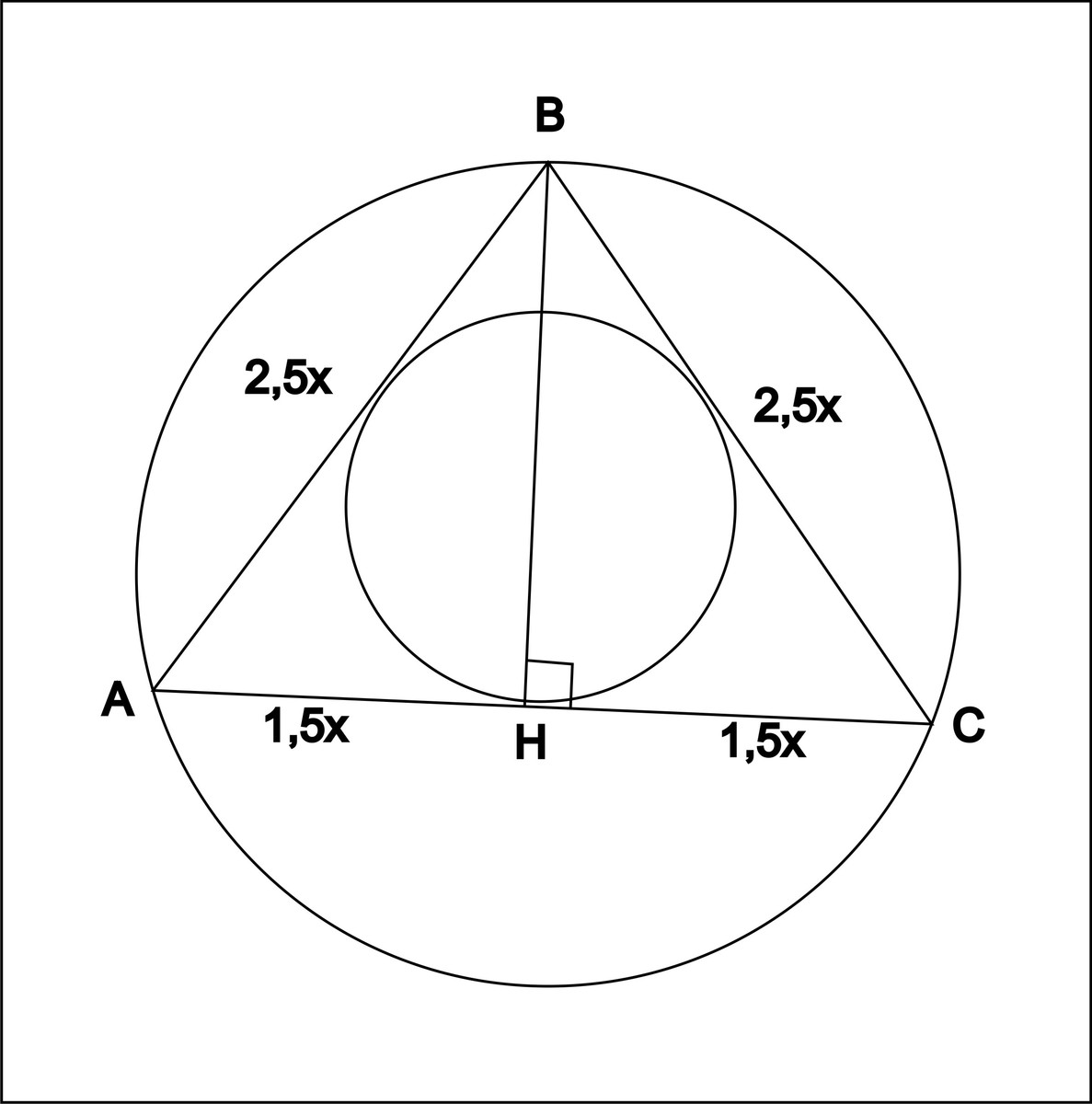
АС- основание
АС=3х
тогда (АВ+ВС+3x)/(3x)=8/3
AB=BC=2,5x
по теореме Пифагора
ВН²=АВ²-АН²
ВН=2х
S(ABC)=(1/2)·BH·AC=(1/2)·2x·3x=3x²
r-радиус вписанной окружности
r=S/p
где р- полупериметр
r=(3x²)/(4x)=(3/4)x
R-радиус описанной окружности
R=(abc)/(4S)=(25/16)x
a,b,c- стороны треугольника
r/R=12/25
АС=3х
тогда (АВ+ВС+3x)/(3x)=8/3
AB=BC=2,5x
по теореме Пифагора
ВН²=АВ²-АН²
ВН=2х
S(ABC)=(1/2)·BH·AC=(1/2)·2x·3x=3x²
r-радиус вписанной окружности
r=S/p
где р- полупериметр
r=(3x²)/(4x)=(3/4)x
R-радиус описанной окружности
R=(abc)/(4S)=(25/16)x
a,b,c- стороны треугольника
r/R=12/25
Приложения:
Похожие вопросы
1 год назад
1 год назад
2 года назад
2 года назад
6 лет назад
8 лет назад
8 лет назад