У трикутнику ABC відомо, що AC= BC, AB=22см, ∠BAC= 30°, відрізок AD — бісектриса трикутника. Знайдіть відрізок AD.
Ответы
Ответ дал:
3
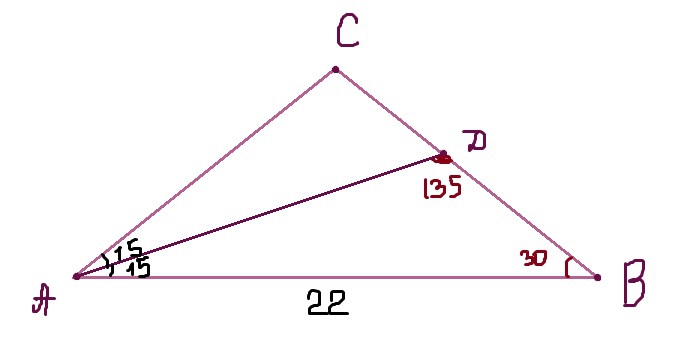
Смотри рисунок.
Рассмотрим
 угол
угол  , угол
, угол  , и легко посчитать угол
, и легко посчитать угол  .
.
Чтобы найти сторону , используем теорему синусов. Формула имеет вид:
, используем теорему синусов. Формула имеет вид:

Формула означает, что отношение каждой стороны треугольника к синусам соответственных противолежащих углов равно.
Теперь посмотрим вновь на наш рисунок, и запишем отношение:

Так как мы знаем два угла и сторону. Можем исключить последнюю дробь.
Получится:


Ответ:
Рассмотрим
Чтобы найти сторону
Формула означает, что отношение каждой стороны треугольника к синусам соответственных противолежащих углов равно.
Теперь посмотрим вновь на наш рисунок, и запишем отношение:
Так как мы знаем два угла и сторону. Можем исключить последнюю дробь.
Получится:
Ответ:
Приложения:
Похожие вопросы
1 год назад
1 год назад
1 год назад
6 лет назад
8 лет назад