Предмет: Алгебра
Автор: Аноним
Вопрос задан 2 года назад

< >

вычислить площадь фигуры, ограниченной линиями у=х^2 , у = -х^2-4x

Ответы

Ответ дал: dnepr1

1

Находим пределы интегрирования:
х² = -х² - 4х
2х² + 4х = 0
х² + 2х = 0
х(х + 2) = 0
х₁ = 0
х₂ = -2.
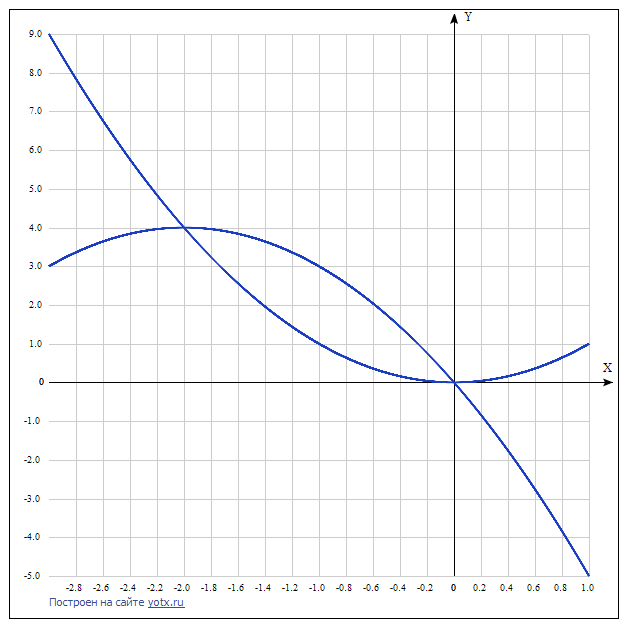
Парабола -х² - 4х проходит выше параболы х²:
$S = \int\limits^0_ {-2} ({-x^2-4x-x^2)} \, dx = \int\limits^0_ {-2} ( {-2x^2-4x)} \, dx =$ $\frac{-2x^3}{3} -2x^2| _{-2}^{0} =-( \frac{-2*(-8)}{3} -2*4)=- \frac{16}{3} +8= \frac{8}{3}$

Приложения:

Похожие вопросы

Математика

1 год назад

Ұшақ A қаласынан B каласына қарай 3сағ12мин ұшты.Белгіленген орынға жету үшін тағы 4 сағ 38 мин артық уакыт ұшуы керек. Ұшақ барлық жолдын неше уакытта ұшып өтеді?

Қазақ тiлi

1 год назад

Қиялдау адам үшін қаншалықты қажет? Қыран жетпеген жерге қиял жетеді дегенді қалай түсінесіңдер?

Русский язык

1 год назад

запиши слова в алфавитном порядке .найди среди перечисленных слов лишнее .делай его звуко буквени разбор .собака, честь,сорока,соловей,сова,сом.

Русский язык

1 год назад

5 предложений придумать 1 - только подлежащее 2 - только сказуемое 3 - и то, и другое 4 - тире между ними 5 - любой оборот тема любая

Алгебра

6 лет назад

Знайдіть найбільший кут трикутника, якщо його сторони дорівнюють 3 см, 5 см і 7 см

Окружающий мир

6 лет назад

2. Закончи предложения. Потомки восточных славян Древняя Русь

Химия

8 лет назад

кислород не взоимодействует с фосфором, азотом, алюминием, фтором

Геометрия

8 лет назад

ПОЖАЛУЙСТА если можете решите хоть что-то из таблицы, нужно мне её заполнить ЭТО ПОСЛЕДНИЙ ШАНС ДЛЯ МЕНЯ!!! На фото рисунок 2. в) изображён вписанный в окружность радиуса R правильный шестиугольник