Образующая конуса равна 12 см и наклонена к основанию под углом 60 градусов. Найдите площадь осевой сечения конуса.

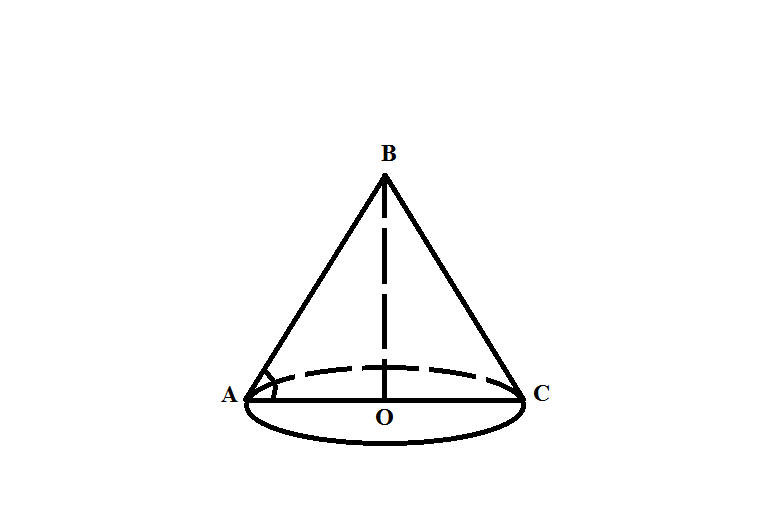
Проведем высоту ВО (см. приложение). Так как угол ОАВ = 60°, а треугольник АВО - прямоугольный, то угол ОАВ = 30°, значит АО = 0,5АВ = 6 см. Найдем катет BO по т. Пифагора:  см. Так как АО = 0,5АС, то АС = 12 см. Треугольник АВС - осевое сечение конуса и его площадь равна: см².
Ответ: 36√3 см²